已知函数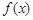 满足对于
满足对于 ,均有
,均有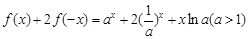 成立.
成立.
(1)求函数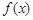 的解析式;
的解析式;
(2)求函数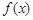 的最小值;
的最小值;
(3)证明: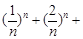 …
…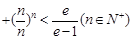 .
.
阅读流程图,若记y=f(x).
(Ⅰ) 写出y=f(x)的解析式,并求函数的值域;
(Ⅱ)若x0满足f(x0)<0 且f(f(x0))=1,求x0.
如图 是单位圆
是单位圆 上的点,且
上的点,且 分别在第一,二象限.
分别在第一,二象限. 是圆与
是圆与 轴正半轴的交点,
轴正半轴的交点, 为正三角形. 若
为正三角形. 若 点的坐标为
点的坐标为 . 记
. 记 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.
(本小题满分10分)
已知极坐标系下曲线 的方程为
的方程为 ,直线
,直线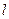 经过点
经过点 ,倾斜角
,倾斜角 .
.
(Ⅰ)求直线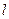 在相应直角坐标系下的参数方程;
在相应直角坐标系下的参数方程;
(Ⅱ)设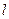 与曲线
与曲线 相交于两点
相交于两点 ,求点
,求点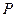 到
到 两点的距离之积.
两点的距离之积.
(本小题满分12分)
已知函数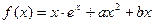 在
在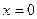 和
和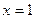 时都取得极值.
时都取得极值.
(Ⅰ)求 和
和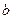 的值;
的值;
(Ⅱ)若存在实数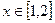 ,使不等式
,使不等式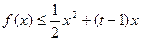 成立,求实数
成立,求实数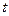 的取值范围;
的取值范围;
(本小题满分12分)
某校举办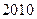 年上海世博会知识竞赛,从参赛的高一、高二学生中各抽
年上海世博会知识竞赛,从参赛的高一、高二学生中各抽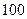 人的成绩作
人的成绩作
 |
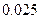 |
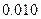 |
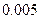 |
 |
 |
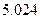 |
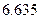 |
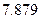 |
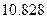 |
为样本,其结果如下表:
参考数据:
| 高一 |
高二 |
合计 |
|
| 合格人数 |
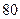 |
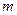 |
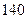 |
| 不合格人数 |
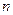 |
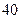 |
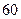 |
| 合计 |
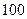 |
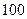 |
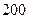 |
(Ⅰ)求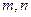 的值;
的值;
(Ⅱ)你有多大的把握认为“高一、高二两个年级这次世博会知识竞赛的成绩有差异”.