已知函数
(1)当 时,求不等式
时,求不等式 的解集; (2)若
的解集; (2)若 的解集包含
的解集包含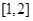 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)
如图所示,动物园要围成相同面积的长方形虎笼四间,一面可以利用原有的墙,其他各面用钢筋网围成。⑴现有可围36m长钢筋网材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?⑵若使每间虎笼面积为24m2,则每间虎笼的长、宽各设计为多少时,可始围成四间虎笼的钢筋网总长最小?
设 的内角
的内角 的对边分别为
的对边分别为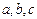 ,且满足
,且满足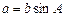 .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)求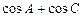 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 ,
,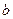 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行.
(I)求实数a的取值范围; (II)是否存在实数a,使得函数
(II)是否存在实数a,使得函数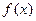 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
在,请说明理由;
(Ⅲ)设
求证: .
.
(本小题满分12分)
已知函数 为奇函数,函数
为奇函数,函数 在区间
在区间 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
(I)求实数 的值;
的值;
(II)求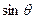 的值及
的值及 的解析式;
的解析式;
(Ⅲ)设 ,试证:对任意的
,试证:对任意的 且
且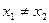 都有
都有 .
.
(本小题满分12分)
关于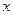 的函数
的函数 与数列
与数列 具有关系:
具有关系: ,
, (
(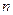 =1,2,3,…)(
=1,2,3,…)( 为常数),又设函数
为常数),又设函数 的导数
的导数 ,
, 为方程
为方程 的实根.
的实根.
(I)用数学归纳法证明: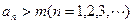 ;
;
(II)证明: .
.