为了了解中学生的体能情况,抽取了某中学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如下图),已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4.第一小组的频数是5.

(1) 求第四小组的频率和参加这次测试的学生人数;
(2) 在这次测试中,学生跳绳次数的中位数落在第几小组内?
(3) 参加这次测试跳绳次数在100次以上为优秀,试估计该校此年级跳绳成绩的优秀率是多少?
(本题满分12分) 本题共有2个小题,第1小题满分5分,第2小题满分7分.
已知函数 ,数列
,数列 满足
满足  ,
, .
.
(1)若数列 是常数列,求a的值;
是常数列,求a的值;
(2)当 时,记
时,记 ,证明数列
,证明数列 是等比数列,并求
是等比数列,并求 .
.
(本小题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分.
已知向量 ,且
,且 .点
.点
(1)求点 的轨迹方程
的轨迹方程 ;
;
(2)过点 且以
且以 为方向向量的一条直线与轨迹方程
为方向向量的一条直线与轨迹方程 相交于点
相交于点 两点,
两点, ,
, 所在的直线的斜率分别是
所在的直线的斜率分别是 、
、 ,求
,求 的值;
的值;
(本小题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分.
已知向量 且与向量
且与向量 夹角为
夹角为 ,其中A,B,C是
,其中A,B,C是 的内角。
的内角。
(1)求角B的大小;
(2)求 的取值范围。
的取值范围。
(本题满分18分,第1小题满分5分,第2小题满分5分,第3小题满分8分)
已知函数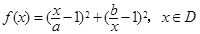 ,其中
,其中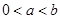 .
.
(1)当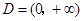 时,设
时,设 ,
,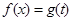 ,求
,求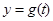 的解析式及定义域;
的解析式及定义域;
(2)当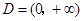 ,
,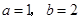 时,求
时,求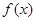 的最小值;
的最小值;
(3)设 ,当
,当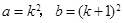 时,
时,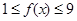 对任意
对任意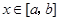 恒成立,求
恒成立,求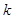 的取值范围.
的取值范围.
(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)
设等比数列 的前
的前 项和为
项和为 ,已知
,已知 .
.
(1)求数列 的通项公式;(2)在
的通项公式;(2)在 与
与 之间插入
之间插入 个1,构成如下的新数列:
个1,构成如下的新数列: ,求这个数列的前
,求这个数列的前 项的和;、(3)在
项的和;、(3)在 与
与 之间插入
之间插入 个数,使这
个数,使这 个数组成公差为
个数组成公差为 的等差数列(如:在
的等差数列(如:在 与
与 之间插入1个数构成第一个等差数列,其公差为
之间插入1个数构成第一个等差数列,其公差为 ;在
;在 与
与 之间插入2个数构成第二个等差数列,其公差为
之间插入2个数构成第二个等差数列,其公差为 ,…以此类推),设第
,…以此类推),设第 个等差数列的和是
个等差数列的和是 . 是否存在一个关于
. 是否存在一个关于 的多项式
的多项式 ,使得
,使得 对任意
对任意 恒成立?若存在,求出这个多项式;若不存在,请说明理由.
恒成立?若存在,求出这个多项式;若不存在,请说明理由.