在
中，两个定点
，的垂心H（三角形三条高线的交点）是AB边上高线CD的中点。
（1）求动点C的轨迹方程；
（2）斜率为2的直线
交动点C的轨迹于P、Q两点，求
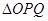面积的最大值（O是坐标原点）。
运货卡车以每小时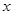
千米的速度匀速行驶130千米
（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油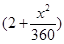
升，司机的工资是每小时14元.
（Ⅰ）求这次行车总费用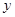
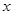关于的表达式；
（Ⅱ）当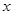为何值时，这次行车的总费用最低，并求出最低费用的值．
在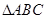
中，角
所对的边分别为
且满足
．
（1）求角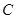
的大小；（2）求
的取值范围.
等差数列
中，
，公差
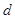为整数，若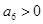
，
．
(2)求前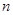
项和
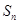的最大值；
等差数列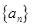
中，
，公差
为整数，若
，
．
(1)求公差的值； (2)求通项公式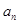
。
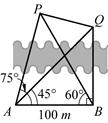
风景秀美的凤凰湖畔有四棵高大的银杏树，记做A、B、P、Q，欲测量P、Q两棵树和A、P两棵树之间的距离，但湖岸部分地方围有铁丝网不能靠近，现在可以方便的测得A、B两点间的距离为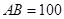
米，如图，同时也能测量出
，
，
，
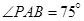，则P、Q两棵树和A、P两棵树之间的距离各为多少？