运货卡车以每小时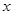 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油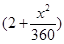 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(Ⅰ)求这次行车总费用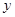 关于
关于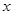 的表达式;
的表达式;
(Ⅱ)当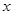 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
数列 的前
的前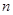 项和为
项和为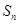 ,且
,且
(1)写出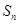 与
与 的递推关系式
的递推关系式 ,并求
,并求 ,
, ,
, 的值;
的值;
(2)猜想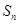 关于
关于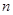 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
已知函数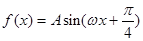 (其中
(其中 ,
, ,
,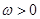 )的最大值为2,最小正周期为
)的最大值为2,最小正周期为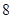 .
.
(1)求函数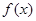 的解析式;
的解析式;
(2)若函数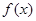 图象上的两点
图象上的两点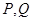 的横坐标依次为
的横坐标依次为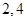 ,
,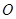 为坐标原点,求
为坐标原点,求
 的值.
的值.
如图,线段 的两个端点
的两个端点 、
、 分别分别在
分别分别在 轴、
轴、 轴上滑动,
轴上滑动, ,点
,点 是
是 上一点,且
上一点,且 ,点
,点 随线段
随线段 的运动而变化.
的运动而变化.
(1)求点 的轨迹方程;
的轨迹方程;
(2)设 为点
为点 的轨迹的左焦点,
的轨迹的左焦点, 为右焦点,过
为右焦点,过 的直线交
的直线交 的轨迹于
的轨迹于 两点,求
两点,求 的最大值,并求此时直线
的最大值,并求此时直线 的方程.
的方程.
已知函数 。
。
(1)若 在
在 处取得极值,求
处取得极值,求 的值;
的值;
(2)求 的单调区间;
的单调区间;
(3)若 且
且 ,函数
,函数 ,若对于
,若对于 ,总存在
,总存在 使得
使得 ,求实数
,求实数 的取值范围。
的取值范围。
设双曲线的顶点为 ,该双曲线又与直线
,该双曲线又与直线 交于
交于 两点,且
两点,且 (
( 为坐标原点)。
为坐标原点)。
(1)求此双曲线的方程;
(2)求