(本小题满分10分)某校要进行特色学校评估验收,有甲、乙、丙、丁、戊五位评估员将随机去 三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
(1)求甲、乙同时去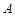 班听课的概率;
班听课的概率;
(2)设随机变量 为这五名评估员去
为这五名评估员去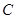 班听课的人数,求
班听课的人数,求 的分布列和数学期望.
的分布列和数学期望.
求函数 (
( )的最小值
)的最小值
数列{ }的前n项和为Sn,已知
}的前n项和为Sn,已知
(Ⅰ)求数列{ }的通项公式;
}的通项公式;
(Ⅱ)若数列{ }满足
}满足 求数列{
求数列{ }的前n项和Tn.
}的前n项和Tn.
(Ⅲ)张三同学利用第(Ⅱ)题中的Tn设计了一个程序流程图,但李四同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束).你是否同意李四同学的观点?请说明理由.
已知椭圆C: (a>b>0)的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(a>b>0)的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点Q(4,0)且不与坐标轴垂直的直线l交椭圆C于A、B两点,设点A关于x轴的对称点为A1.求证:直线A1B过x轴上一定点,并求出此定点坐标.
若函数f(x)=
(Ⅰ)当a=2时,求函数f(x)的单调增区间;
(Ⅱ)函数f(x)是否存在极值.
一个多面体的直观图和三视图如图所示,其中M,N分别是AB,AC的中点,G是DF上的一动点.
(Ⅰ)求证:GN⊥AC;
(Ⅱ)若点G是DF的中点,求证:GA∥平面FMC.