已知函数 .
(1)设 .
①求方程 的根;
②若对任意 , 不等式 恒成立, 求实数 的最大值;
(2)若 , 函数 有且只有 1 个零点, 求 的值。
(本小题满分12分)
(1)设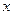 是正实数,求证:
是正实数,求证: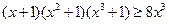 ;
;
(2)若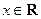 ,不等式
,不等式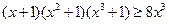 是否仍然成立?如果成立,请给出证明;如果不成立,请举出一个使它不成立的
是否仍然成立?如果成立,请给出证明;如果不成立,请举出一个使它不成立的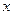 的值.
的值.
(本小题满分12分) 数列
数列 的前
的前 项和为
项和为 且
且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)等差数列 的各项均为正数,其前
的各项均为正数,其前 项和为
项和为 ,
, ,又
,又 成等比数列,求
成等比数列,求 .
.
(本小题满分12分)
已知函数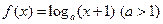 ,函数
,函数 的图象与函数
的图象与函数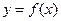 的图象关于原点对称.若
的图象关于原点对称.若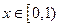 时,总有
时,总有 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)
已知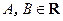 ,且
,且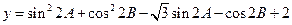 .
.
(1)若 为
为 的三内角,当
的三内角,当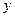 取得最小值时
取得最小值时 ,求
,求 ;
;
(2)当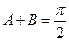 时,将函数
时,将函数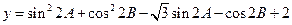 的图象按向量
的图象按向量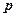 平移后得到函数
平移后得到函数 的图象,求出所有满足条件的向量
的图象,求出所有满足条件的向量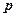 .
.
附加 题:(本小题10分,实验班同学必做,其他班学生选做)
题:(本小题10分,实验班同学必做,其他班学生选做)
是否存在常数a,使得函数f (x)=sin2x+acosx+ -
- 在闭区间
在闭区间 上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值为1?若存在,求出对应的a值;若不存在,说明理由.