直线y=2x+3与抛物线y=ax2交于A、B两点,已知点A的横坐标是3,求A、B两点坐标及抛物线的函数关系式.
(本题满分9分)
如图11,已知抛物线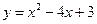 与x 轴交于两点A、B,其顶点为C.
与x 轴交于两点A、B,其顶点为C.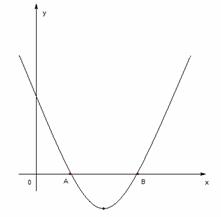
(1)对于任意实数m,点M(m,-2)是否在该抛物线上?请说明理由;
(2)求证:△ABC是等腰直角三角形;
(3)已知点D在x轴上,那么在抛物线上是否存在点P,使得以B、C、D、P为顶点的四边形是 平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
(本题满分9分)如图9,已知线段AB的长为2a,点P是AB上的动点(P不与A,B重合),分别以AP、PB为边向线段AB的同一侧作正△APC和正△PBD.
(1)当△APC与△PBD的面积之生取最小值时,AP= ;(直接写结果)
;(直接写结果)
(2)连结AD、BC,相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动面变化?请说明理由;
(3)如图10,若点P固定,将△PBD绕点P按顺时针方向旋转(旋转角小于 180°),此时α的大小是否发生变化?(只需直接写出你的猜想,不必证明)
180°),此时α的大小是否发生变化?(只需直接写出你的猜想,不必证明)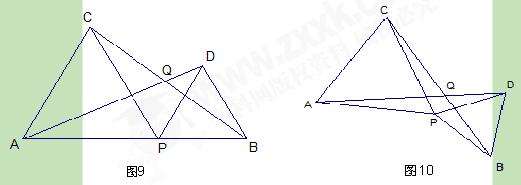
(本题满分9分) 如图8,等腰梯形ABCD中,AB∥CD,AD=BC.将△ACD沿对角线AC翻折后,点D恰好与边AB的中点M重合.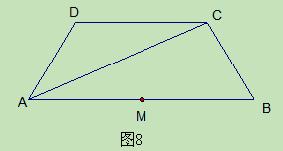
(1)点C是否在以AB为直径的圆上?请说明理由;
(2)当AB=4时,求此梯形的面积.
(本题满分7分)
为了鼓励城区居民节约用水,某市规定用水收费标准如下:每户每月的用水量不超过20度时(1度=1米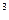 ),水费为a元/度;超过20度时,不超过部分仍为a元/度,超过部分为b元/度.已知某用户四份用水15度,交水费22.5元,五月份用水30度,交水费50元.
),水费为a元/度;超过20度时,不超过部分仍为a元/度,超过部分为b元/度.已知某用户四份用水15度,交水费22.5元,五月份用水30度,交水费50元.
(1)求a,b的值;
(2)若估计该用户六月份的水费支出不少于60元,但不超过90元,求该用户六月份的用水量x的取值范围.
(本题满分7分.)如图7,反比例函数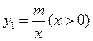 的图像与一次函数
的图像与一次函数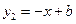 的图象交于点A、B,其中A(1,2).
的图象交于点A、B,其中A(1,2).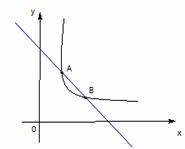
(1)求m,b的值;
(2)求点B的坐标,并写出 时,
时,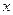 的取值范
的取值范 围.
围.