(本题满分7分)
为了鼓励城区居民节约用水,某市规定用水收费标准如下:每户每月的用水量不超过20度时(1度=1米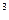 ),水费为a元/度;超过20度时,不超过部分仍为a元/度,超过部分为b元/度.已知某用户四份用水15度,交水费22.5元,五月份用水30度,交水费50元.
),水费为a元/度;超过20度时,不超过部分仍为a元/度,超过部分为b元/度.已知某用户四份用水15度,交水费22.5元,五月份用水30度,交水费50元.
(1)求a,b的值;
(2)若估计该用户六月份的水费支出不少于60元,但不超过90元,求该用户六月份的用水量x的取值范围.
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),
将△ABC绕点A按逆时针方向旋转90°得到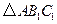 .(1)在正方形网格中,作出
.(1)在正方形网格中,作出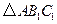 ;(不要求写作法)(2)设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形, 然后求出它的面积.(结果保留
;(不要求写作法)(2)设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形, 然后求出它的面积.(结果保留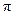 )
)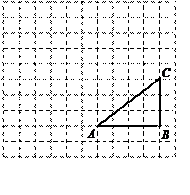
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=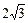 ,直线y=
,直线y= 经过点C,交y轴于点G,且∠AGO=30°。
经过点C,交y轴于点G,且∠AGO=30°。
(1)点C、D的坐标分别是C(),D();
(2)求顶点在直线y= 上且经过点C、D的抛物线的解析式;
上且经过点C、D的抛物线的解析式;
(3)将(2)中的抛物线沿直线y=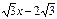 平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存
平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存 在,请求出此时抛物线的解析式;若不存在,请说明理由。
在,请求出此时抛物线的解析式;若不存在,请说明理由。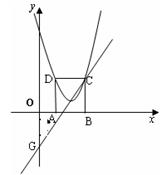
某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为: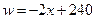 ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式;
(2)当x取何值时,y的值最大?
(3)如果公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
有A、B两个黑布袋,A布袋中有两个完全相同的小球,分
别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字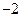 ,
,
和-4.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B
布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐
标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=-X-2上的概率
如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线 ,其中
,其中 (m)是球的飞行高度,
(m)是球的飞行高度, (m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(1)请写出抛物线的开口方向、顶点坐标、对称轴.
(2)请求出球飞行的最大水平距离.
(3)若王强再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线,求出其解析式