设数列 为单调递增的等差数列
为单调递增的等差数列 且
且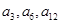 依次成等比数列.
依次成等比数列.
(Ⅰ)求数列 的通项公式
的通项公式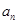 ;
;
(Ⅱ)若 求数列
求数列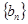 的前
的前 项和
项和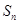 ;
;
(Ⅲ)若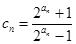 ,求证:
,求证: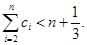
已知函数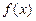 是定义在
是定义在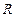 上的偶函数,当
上的偶函数,当 时,
时, .
.
(1)求当 时
时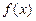 的解析式;
的解析式;
(2)试确定函数 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;
(3)若 且
且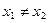 ,证明:
,证明: .
.
记函数 ,
, ,它们定义域的交集为
,它们定义域的交集为 ,若对任意的
,若对任意的 ,
, ,则称
,则称 是集合
是集合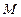 的元素.
的元素.
(1)判断函数 是否是
是否是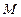 的元素;
的元素;
(2)设函数 ,求
,求 的反函数
的反函数 ,并判断
,并判断 是否是
是否是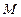 的元素;
的元素;
已知抛物线 与直线
与直线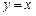 相切于点
相切于点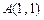 .
.
(Ⅰ)求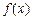 的解析式;
的解析式;
(Ⅱ)若对任意 ,不等式
,不等式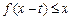 恒成立,求实数
恒成立,求实数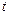 的取值范围.
的取值范围.
在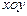 平面上有一系列点
平面上有一系列点
 对每个自然数
对每个自然数 ,点
,点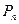 位于函数
位于函数 的图象上.以点
的图象上.以点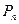 为圆心的⊙
为圆心的⊙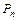 与
与 轴都相切,且⊙
轴都相切,且⊙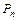 与⊙
与⊙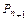 又彼此外切.若
又彼此外切.若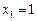 ,且
,且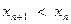
 .
.
(1)求证:数列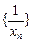 是等差数列;
是等差数列;
(2)设⊙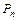 的面积为
的面积为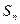 ,
, , 求证:
, 求证:
如图直角梯形OABC中,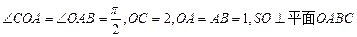 ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
(Ⅰ)求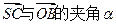 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(Ⅱ)设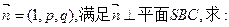
①
②OA与平面SBC的夹角 (用反三角函数表示);
(用反三角函数表示);
③O到平面SBC的距离.
(Ⅲ)设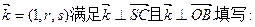
①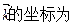 .
.
②异面直线SC、OB的距离为.
(注:(Ⅲ)只要求写出答案).