在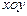 平面上有一系列点
平面上有一系列点
 对每个自然数
对每个自然数 ,点
,点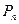 位于函数
位于函数 的图象上.以点
的图象上.以点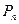 为圆心的⊙
为圆心的⊙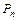 与
与 轴都相切,且⊙
轴都相切,且⊙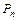 与⊙
与⊙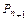 又彼此外切.若
又彼此外切.若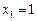 ,且
,且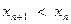
 .
.
(1)求证:数列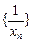 是等差数列;
是等差数列;
(2)设⊙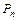 的面积为
的面积为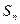 ,
, , 求证:
, 求证:
(本小题满分12分)已知函数 的最大值为2,且最小正周期为
的最大值为2,且最小正周期为 .
.
(1)求函数 的解析式及其对称轴方程;
的解析式及其对称轴方程;
(2)若 的值.
的值.
(本小题满分12分)某中学在高二年级开设大学先修课程《线性代数》,共有50名同学选修,其中男同学30名,女同学20名.为了对这门课程的教学效果进行评估,学校按性别采用分层抽样的方法抽取5人进行考核.
(1)求抽取的5人中男、女同学的人数;
(2)考核前,评估小组打算从抽取的5人中随机选出2名同学进行访谈,求选出的两名同学中恰有一名女同学的概率.
(本小题满分14分)已知椭圆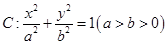 ,其中
,其中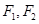 为左、右焦点,O为坐标原点.直线l与椭圆交于
为左、右焦点,O为坐标原点.直线l与椭圆交于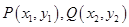 两个不同点.当直线l过椭圆C右焦点F2且倾斜角为
两个不同点.当直线l过椭圆C右焦点F2且倾斜角为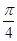 时,原点O到直线l的距离为
时,原点O到直线l的距离为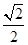 .又椭圆上的点到焦点F2的最近距离为
.又椭圆上的点到焦点F2的最近距离为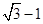 .
.
(1)求椭圆C的方程;
(2)以OP,OQ为邻边做平行四边形OQNP,当平行四边形OQNP面积为 时,求平行四边形OQNP的对角线之积
时,求平行四边形OQNP的对角线之积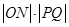 的最大值;
的最大值;
(3)若抛物线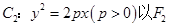 为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
(本小题满分13分)已知函数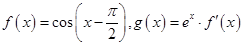 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求曲线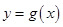 在点
在点 处的切线方程;
处的切线方程;
(2)若对任意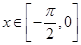 ,不等式
,不等式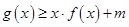 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)试探究当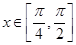 时,方程
时,方程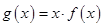 的解的个数,并说明理由.
的解的个数,并说明理由.
(本小题满分12分)已知数列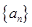 中,
中,
(1)求证:数列 是等比数列;
是等比数列;
(2)若 是数列
是数列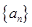 的前n项和,求满足
的前n项和,求满足 的所有正整数n.
的所有正整数n.