(本小题满分12分)甲,乙两人约定上午7:00至8:00之间到某站乘公共汽车,在这段时间内有2班公共汽车,它们开车的时刻分别是7:30和8:00,甲、乙两人约定,见车就乘,则甲、乙同乘一车的概率为(假定甲、乙两人到达车站的时刻是互相不牵连的,且每人在7时到8时的任何时刻到达车站是等可能的).
(本小题满分14分)已知椭圆的中心在原点,焦点在 轴上,离心率为
轴上,离心率为 ,且经过点
,且经过点 . 直线
. 直线 交椭圆于不同的两点
交椭圆于不同的两点 .
.
(1)求椭圆的方程;
(2)求 的取值范围;
的取值范围;
(3)若直线 不过点
不过点 ,求证:直线
,求证:直线 与
与 轴围成一个等腰三角形.
轴围成一个等腰三角形.
(本小题满分14分)若正项数列 的前
的前 项和为
项和为 ,首项
,首项 ,点
,点 (
( )在曲线
)在曲线 上.源:
上.源:
(1)求数列 的通项公式
的通项公式 ;
;
(2)设 ,
, 表示数列
表示数列 的前
的前 项和,求证:
项和,求证: .
.
(本小题满分14分)
如图所示,在所有棱长都为 的三棱柱
的三棱柱 中,侧棱
中,侧棱 ,
, 点为棱
点为棱 的中点.
的中点.
(1)求证: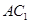 ∥平面
∥平面 ;
;
(2)求四棱锥 的体积.
的体积.
(本小题满分12分)某班 名学生在一次百米测试中,成绩全部介于
名学生在一次百米测试中,成绩全部介于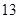 秒与
秒与 秒之间,将测试结果按如下方式分成五组:第一组
秒之间,将测试结果按如下方式分成五组:第一组 ,第二组
,第二组 , ,第五组
, ,第五组 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.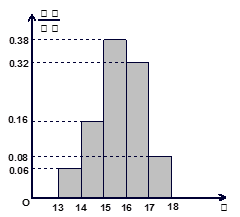
(1)根据频率分布直方图,估计这 名学生百米测试成绩的平均值;
名学生百米测试成绩的平均值;
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于 的概率.
的概率.
(本小题满分12分)已知函数
 的最小正周期为
的最小正周期为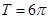 ,且
,且 .
.
(1)求 的表达式;
的表达式;
(2)设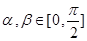 ,
, ,
, ,求
,求 的值.
的值.