如图,在平面直角坐标系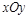
中,以
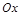轴为始边作两个锐角
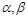,它们的终边分别与单位圆交于
两点.已知两点的纵坐标分别为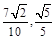
.
(1)求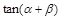
的值；
(2)求角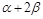
的大小.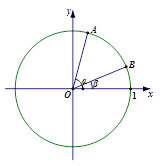
已知函数
（
为常数）是实数集
上的奇函数．
（1）求实数的值；
（2）讨论关于
的方程
的根的个数；
（3）证明：
．
设函数
，其中
．
（1）当
时，判断函数
在定义域上的单调性；
（2）求函数的极值点．
已知数列
的前
项和为
，且满足
．
（1）求证：数列
是等比数列，并求数列的通项公式；
（2）求证：
．
已知单调递增的等比数列
满足：
，且
是
，
的等差中项．
（1）求数列的通项公式；
（2）若
，
，求
成立的正整数
的最小值．
已知函数
，直线
，
是
图象的任意两条对称轴，且
的最小值为
．
（1）求
的表达式；
（2）将函数的图象向右平移
个单位后，再将得到的图象上各点的横坐标伸长为原来的2倍，纵坐
标不变，得到函数
的图象，若关于
的方程
，在区间
上有且只有一个实数解，求实数
的取值范围．