(本小题满分14分)已知函数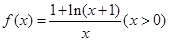 .
.
(Ⅰ)函数 在区间
在区间 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;
(Ⅱ)当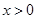 时,
时,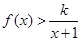 恒成立,求整数
恒成立,求整数 的最大值;
的最大值;
(Ⅲ)试证明: .
.
已知函数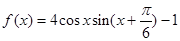 .
.
(1)求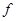 (x)的最小正周期和单调递增区间;
(x)的最小正周期和单调递增区间;
(2)求f(x)在区间 上的最大值和最小值.
上的最大值和最小值.
(本小题满分10分)选修4-4:极坐标与参数方程选讲
已知曲线 的极坐标方程是
的极坐标方程是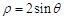 ,直线
,直线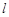 的参数方程是
的参数方程是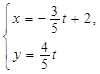 (
(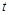 为参数).
为参数).
(Ⅰ)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)设直线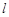 与
与 轴的交点是
轴的交点是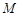 ,
, 是曲线
是曲线 上一动点,求
上一动点,求 的最大值.
的最大值.
(本小题满分10分)选修4-1几何证明选讲
已知
 外接圆劣弧
外接圆劣弧 上的点(不与点
上的点(不与点 、
、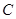 重合),延长
重合),延长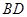 至
至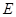 ,延长
,延长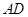 交
交 的延长线于
的延长线于 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求证: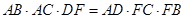 .
.
已知函数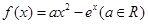
(Ⅰ)当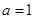 时,判断函数
时,判断函数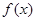 的单调区间并给予证明;
的单调区间并给予证明;
(Ⅱ)若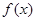 有两个极值点
有两个极值点 ,证明:
,证明: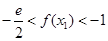 .
.
(本小题满分12分)已知抛物线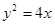 ,直线
,直线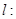
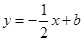 与抛物线交于
与抛物线交于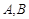 两点.
两点.
(Ⅰ)若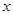 轴与以
轴与以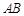 为直径的圆相切,求该圆的方程;
为直径的圆相切,求该圆的方程;
(Ⅱ)若直线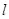 与
与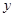 轴负半轴相交,求
轴负半轴相交,求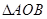 面积的最大值.
面积的最大值.