(本小题12分)已知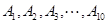 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为 .
.
(Ⅰ)如果该同学10所高校的考试都参加,试求恰有2所通过的概率;
(Ⅱ)假设该同学参加每所高校考试所需的费用均为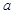 元,该同学决定按
元,该同学决定按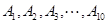 顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试,试求该同学参加考试所需费用
顺序参加考试,一旦通过某所高校的考试,就不再参加其它高校的考试,试求该同学参加考试所需费用 的分布列及数学期望.
的分布列及数学期望.
某工厂计划生产甲、乙两种产品,这两种产品都需要两种原料。生产甲产品1工时需要A种原料3kg,B种原料1 kg;生产乙产品1工时需要A种原料2kg,B种原料2kg。现有A种原料1200 kg,B种原料800 kg。如果生产甲产品每工时的平均利润是30元,生产乙产品每工时的平均利润是40元,问甲、乙两种产品各生产多少工时能使利润的总额最大?最大利润是多少?
在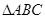 中内角
中内角 的对边分别为
的对边分别为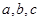 ,且
,且 ,
,
(1)求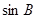 的值;
的值;
(2)如果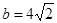 ,且
,且 ,求
,求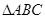 的面积.
的面积.
已知 ,解关于
,解关于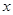 的不等式
的不等式 <
<
设
(1)求函数 的解析式.
的解析式.
(2)已知常数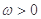 , 若
, 若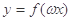 在区间
在区间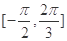 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.
(3)设集合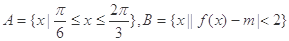 ,若
,若 ,求实数
,求实数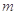 的取值范围.
的取值范围.
已知向量 且
且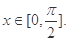 求:
求:
(1)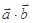 及
及
(2)若函数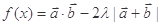 的最小值为
的最小值为 求实数
求实数 的值。
的值。