如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A,B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD,CD.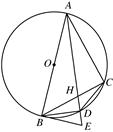
(1)求证:BD平分∠CBE;
(2)求证:AH·BH=AE·HC.
(本小题满分12分)一袋子中有大小、质量均相同的10个小球,其中标记“开”字的小球有5个,标记“心”字的小球有3个,标记“乐”字的小球有2个.从中任意摸出1个球确定标记后放回袋中,再从中任取1个球.不断重复以上操作,最多取3次,并规定若取出“乐”字球,则停止摸球.求:
(Ⅰ)恰好摸到2个“心”字球的概率;
(Ⅱ)摸球次数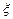 的概率分布列和数学期望.
的概率分布列和数学期望.
(本小题满分10分)在 中,
中, 、
、 、
、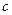 分别是三内角
分别是三内角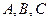 的对应的三边,已知
的对应的三边,已知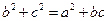 。
。
(Ⅰ)求角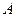 的大小;
的大小;
(Ⅱ)若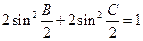 ,判断
,判断 的形状。
的形状。
(本小题满分13分)
设函数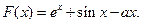
(1)若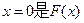 的极值点,求实数a的值;
的极值点,求实数a的值;
(2)若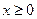 时,函数
时,函数 图象恒不在
图象恒不在 图象的下方,求实数a的取值范围。
图象的下方,求实数a的取值范围。
(本小题满分13分)工厂生产某种产品,次品率p与日产量x(万件)间的关系为: (c为常数, 且0<c<6).已知每生产1件合格产品盈利3元,
(c为常数, 且0<c<6).已知每生产1件合格产品盈利3元,
每出现1件次品亏损1.5元.
(1)将日盈利额y(万元)表示为日产量x(万件)的函数;
(2)为使日盈利额最大,日产量应为多少万件?(注:次品率=×100%)
(本小题满分12分)
设函数 (0<
(0<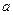 <1).
<1).
(1)求函数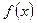 的单调区间;
的单调区间;
(2)若当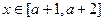 时,恒有
时,恒有 成立,试确定
成立,试确定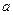 的取值范围.
的取值范围.