（本小题满分12分）一袋子中有大小、质量均相同的10个小球，其中标记“开”字的小球有5个，标记“心”字的小球有3个，标记“乐”字的小球有2个．从中任意摸出1个球确定标记后放回袋中，再从中任取1个球．不断重复以上操作，最多取3次，并规定若取出“乐”字球，则停止摸球．求：
（Ⅰ）恰好摸到2个“心”字球的概率；
（Ⅱ）摸球次数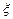
的概率分布列和数学期望．
已知函数f(x)=x
+x－16.
(1)求曲线y=f(x)在点(2,－6)处的切线方程;
(2)直线ｌ为曲线y=f(x)的切线,且经过原点,求直线ｌ的方程及切点坐标
已知函数f(x)＝
是定义在(－1,1)上的奇函数，且
f(
)＝
.
(1)求函数f(x)的解析式；
(2)用定义证明f(x)在(－1,1)上是增函数；
(3)解不等式f(t－1)＋f(t)<0.
已知f(x)＝logax(a>0且a≠1)，如果对于任意的x∈[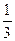
，2]都有|f(x)|≤1
成立，试求a的取值范围
已知f(x)
＝x2＋2x－5，x∈[t，t＋1]，若f(x)的最小值为h(t)，写出h(t)的表达式．
命题p：关于x的不等式x2＋2ax＋4>0，对一切x∈R恒成立，q：函数f(
x)＝(3－2a)x是增函数，若p或q为真，p且q为假，求实数a的取值范围．