(本小题12分)在直三棱柱(侧棱垂直底面) 中,
中,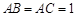 ,
, .
.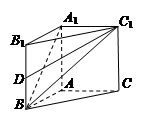
(Ⅰ)若异面直线 与
与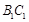 所成的角为
所成的角为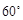 ,求棱柱的高;
,求棱柱的高;
(Ⅱ)设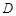 是
是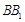 的中点,
的中点,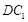 与平面
与平面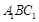 所成的角为
所成的角为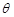 ,当棱柱的高变化时,求
,当棱柱的高变化时,求 的最大值.
的最大值.
(本小题满分13分)已知等比数列 的公比为
的公比为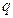 ,前
,前 项和为
项和为 ,且
,且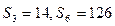 ,现若以
,现若以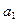 为首项
为首项 ,以公比
,以公比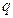 作为公差d构造新的等差数列
作为公差d构造新的等差数列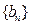
(1)求通项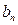 (2)记
(2)记 ,证明
,证明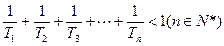
(本小题满分12分)已知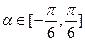 且
且 ,请求出
,请求出 与
与 的值
的值
(本小题满分12分)如图所示,△ABC中,∠A=60°、∠C=45°,BC=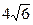 ,现点D在AC边上运动,点E在AB边上运动(不与端点重合)且AD=BE=
,现点D在AC边上运动,点E在AB边上运动(不与端点重合)且AD=BE= ,设△ADE面积为S
,设△ADE面积为S
(1)写出函数式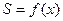 ,并标出定义域。
,并标出定义域。
(2)求出 取何值时,S有最大值,并求之。
取何值时,S有最大值,并求之。
(本小题满分12分)函数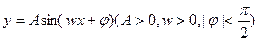 的图像上相邻的最高点与最低点的坐标分别为
的图像上相邻的最高点与最低点的坐标分别为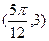 和
和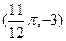 。 (1)求出
。 (1)求出 的解析式。(2)找出
的解析式。(2)找出 图像的对称中心和
图像的对称中心和 的递增区间。
的递增区间。
四棱锥S-ABCD的底面是边长为1的正方形,侧棱SB垂直于底面,并且SB= ,用
,用 表示∠ASD,求
表示∠ASD,求