已知：如图，把矩形OCBA放置于直角坐标系中，OC=3，BC=2，取AB的中点M，连结MC，把△MBC沿x轴的负方向平移OC的长度后得到△DAO.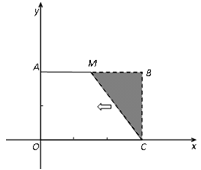
（1）直接写出点D的坐标；
（2）已知点B与点D在经过原点的抛物线上，点P在第一象限内的该抛物线上移动，过点P作PQ⊥x轴于点Q，连结OP.
①若以O、P、Q为顶点的三角形与△DAO相似，试求出点P的坐标；
②试问在抛物线的对称轴上是否存在一点T，使得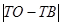
的值最大.若存在，求出T点坐标；若不存在，请说明理由.
（1）用配方法解方程：
;
（2）用公式法解方程：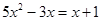
.
抛物线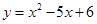
与
轴交于
两点，则
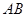的长为．
如图，在△ABC中，∠C=90°，∠CAD=∠BAD，DE⊥AB于E，点F在边AC上，连接DF．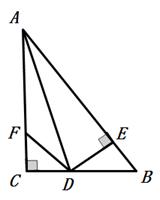
（1）求证：AC=AE；
（2）若AC=8，AB=10，且△ABC的面积等于24，求DE的长；
（3）若CF=BE，直接写出线段AB，AF，EB的数量关系：．
观察下列等式：
1×3+1=22
3×5+1=42
5×7+1=62
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．
请你按照上述三个等式的规律写出第④个、第⑤个等式；
请猜想，第n个等式（n为正整数）应表示为；
证明你猜想的结论．
如图，在△ABC中，∠ABC与∠ACB的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．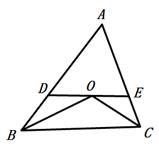
（1）若AB=7，AC=5，求△ADE的周长；
（2）若∠ABC=∠ACB，AC=10，直接写出图中所有的等腰三角形并求△ADE的周长．