(本小题满分12分）
PM2. 5是指大气中直径小于或等于2. 5微米的颗粒物，也称为 可人肺颗粒物.我国PM2. 5标准采用世卫组织设定的最宽限 值，即PM2.5日均值在35微克/立方米以下空气质量为一级； 在35微克/立方米~75微克/立方米之间空气质量为二级；在 75微克/立方米以上空气质量为超标.
某市环保局从市区2012年全年每天的PM2.5监测数据中 随机抽取15天的数据作为样本，监测值如茎叶图所示（十位为 茎，个位为叶）
(I)从这9天的数据中任取2天的数据，求恰有一天空气质量达到一级的概率；
(II) 以这9天的PM2. 5日均值来估计供暖期间的空气质量情况，则供暖期间(按150天计算）中大约有多少天的空气质量达到一级.
有甲乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的列联表.
| 优秀 |
非优秀 |
总计 |
|
| 甲班 |
10 |
||
| 乙班 |
30 |
||
| 合计 |
105 |
已知在全部105人中抽到随机抽取1人为优秀的概率为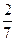
(Ⅰ)请完成上面的列联表；
(Ⅱ)根据列联表的数据，若按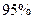
的可靠性要求，能否认为“成绩与班级有关系”.
(Ⅲ)若按下面的方法从甲班优秀的学生抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
某中学在高一开设了数学史等4门不同的选修课，每个学生必须选修，有只能从中选一门。该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同。（Ⅰ）求3个学生选择了3门不同的选修课的概率；（Ⅱ）求恰有2门选修课这3个学生都没有选择的概率；（Ⅲ）设随机变量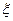
为甲、乙、丙这三个学生选修数学史这门课的人数，求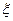的分布列
与数学期望。
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：
| 日期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
温差 （°C） |
10 |
11 |
13 |
12 |
8 |
发芽数 （颗） |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这五组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．（1）求选取的2组数据恰好是不相邻2天数据的概率；（2）若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求出y关于x的线性回归方程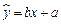
；
（3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（2）中所得的线性回归方程是否可靠?
某单位要在甲、乙、丙、丁4人中安排2人分别担任周六、周日的值班任务（每人被安排是等可能的，每天只安排一人）。求：（1）其中甲、乙两人都被安排的概率是多少？（2）甲、乙两人中至少有一人被安排的概率是多少？
甲从装有编号为1，2，3，4，5的卡片的箱子中任意取一张，乙从装有编号为2，4的卡片的箱子中任意取一张，用
，分别表示甲、乙取得的卡片上的数字.（1）求概率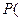
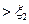）；（2）记
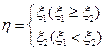，求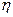
的分布列与数学期望.