设点P(x,y)在椭圆 上,求
上,求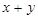 的最大、最小值.
的最大、最小值.
(12分)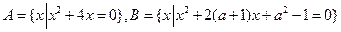 ,其中
,其中 ,如果
,如果 ,求实数
,求实数 的取值范围。
的取值范围。
已知函数 ,在点(1,f(1))处的切线方程为y+2=0.
,在点(1,f(1))处的切线方程为y+2=0.
(1) 求函数f(x)的解析式;
(2) 若对于区间[一2,2]上任意两个自变量的值x1,x2,都有 ,求实
,求实
数c的最小值;
(3) 若过点M(2,m)(m≠2),可作曲线y=f(x)的三条切线,求实数m的取值范围,
已知椭圆C的中心在原点,焦点在x轴上,左右焦点分别为F1,F2;且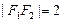
点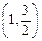 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A、B两点,且△AF2B的面积为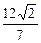 ,求以F2为圆
,求以F2为圆
心且与直线l相切的圆的方程.
己知数列 满足:
满足: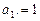 ,
,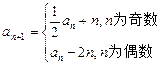
(1) 求a2,a3;
(2) 设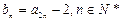 ,求证
,求证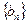 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(3) 在(2)条件下,求数列 前100项中的所有偶数项的和S。
前100项中的所有偶数项的和S。
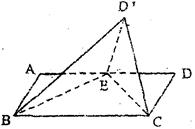
已知矩形ABCD,AD=2AB=2,点E是AD的中点,将△DEC
沿CE折起到△D’EC的位置,使二面角D'-EC -B是直二面角。
(Ⅰ) 证明:BE⊥CD’;
(Ⅱ) 求二面角D'-BC -E的余弦值,