(本小题满分12分)
正项数列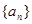 的首项为
的首项为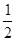 ,
,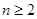 时,
时, ,数列
,数列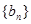 对任意
对任意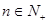 均有
均有
(1)若 ,求证:数列
,求证:数列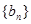 是等差数列;
是等差数列;
(2)已知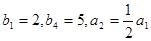 ,数列
,数列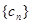 满足
满足 ,记数列
,记数列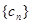 的前
的前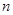 项和为
项和为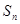 ,求证
,求证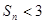 .
.
已知函数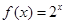 ,
, .
.
(Ⅰ)解方程: ;
;
(Ⅱ)设 ,求函数
,求函数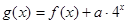 在区间
在区间 上的最大值
上的最大值 的表达式;
的表达式;
(Ⅲ)若 ,
, ,求
,求 的最大值.
的最大值.
已知椭圆具有性质:若 是椭圆
是椭圆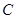 :
: 且
且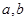 为常数
为常数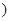 上关于原点对称的两点,点
上关于原点对称的两点,点 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线 和
和 的斜率都存在,并分别记为
的斜率都存在,并分别记为 ,
, ,那么
,那么 与
与 之积是与点
之积是与点 位置无关的定值
位置无关的定值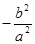 .
.
试对双曲线 且
且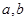 为常数
为常数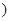 写出类似的性质,并加以证明.
写出类似的性质,并加以证明.
为了提高产品的年产量,某企业拟在2013年进行技术改革.经调查测算,产品当年的产量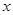 万件与投入技术改革费用
万件与投入技术改革费用 万元(
万元(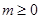 )满足
)满足 (
( 为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定收入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的
为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定收入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的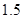 倍(生产成本包括固定投入和再投入两部分资金).
倍(生产成本包括固定投入和再投入两部分资金).
(Ⅰ)试确定的 值,并将2013年该产品的利润
值,并将2013年该产品的利润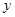 万元表示为技术改革费用
万元表示为技术改革费用 万元的函数(利润=销售金额―生产成本―技术改革费用);
万元的函数(利润=销售金额―生产成本―技术改革费用);
(Ⅱ)该企业2013年的技术改革费用投入多少万元时,厂家的利润最大?
已知定义域为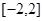 的函数
的函数 是奇函数.
是奇函数.
(Ⅰ)求实数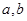 的值;(Ⅱ)解关于
的值;(Ⅱ)解关于 的不等式
的不等式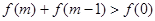 .
.
设命题p:函数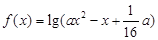 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式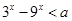 对任意
对任意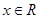 恒成立.
恒成立.
(Ⅰ)如果p是真命题,求实数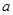 的取值范围;
的取值范围;
(Ⅱ)如果命题“p或q”为真命题且“p且q”为假命题,求实数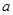 的取值范围.
的取值范围.