(本小题满分12分）
某市的教育研究机构对全市高三学生进行综合素质 测试，随机抽取了部分学生的成绩，得到如图所示的成绩 频率分布直方图.
(I )估计全市学生综合素质成绩的平均值；
(II)若评定成绩不低于8o分为优秀.视频率为概率，从 全市学生中任选3名学生(看作有放回的抽样），变量
表示 3名学生中成绩优秀的人数，求变量的分布列及期望
)
解关于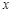
的不等式：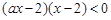
解不等式
（1）已知关于x的不等式(a＋b)x＋(2a－3b)<0的解集为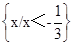
，求关于x的不等式(a－3b)x＋(b－2a)>0的解集．
（2）
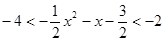
(10分) 已知数列{an}的前n项和Sn＝10n－n2，(n∈N*)．
(1)求a1和an；
(2)记bn＝|an|，求数列{bn}的前n项和．
已知函数
（
）
（Ⅰ）讨论
的单调性；
（Ⅱ）当
时，设
，若存在
,
，使
，
求实数
的取值范围。
为自然对数的底数，
已知椭圆
上的动点到焦点距离的最小值为
。以原点为圆心、椭圆的短半轴长为半径的圆与直线
相切．
（Ⅰ）求椭圆
的方程；
（Ⅱ）若过点
(2，0)的直线与椭圆相交于
两点，
为椭圆上一点， 且满足
（
为坐标原点）。当
时，求实数
的值．