已知椭圆
 上的动点到焦点距离的最小值为
上的动点到焦点距离的最小值为 。以原点为圆心、椭圆的短半轴长为半径的圆与直线
。以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于
相交于 两点,
两点, 为椭圆上一点, 且满足
为椭圆上一点, 且满足 (
( 为坐标原点)。当
为坐标原点)。当 时,求实数
时,求实数 的值.
的值.
观察下面一组组合数等式: ;
; ;
; ;
;
…………
(1)由以上规律,请写出第 个等式并证明;
个等式并证明;
(2)随机变量 ,求证:
,求证: .
.
正四面体 边长为2.
边长为2.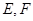 分别为
分别为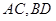 中点.
中点.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
设函数 .
.
(1)若函数 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
在平面直角坐标系 中,点P到两圆C1与C2的圆心的距离之和等于4,其中C1:
中,点P到两圆C1与C2的圆心的距离之和等于4,其中C1: ,C2:
,C2: . 设点P的轨迹为
. 设点P的轨迹为 .
.
(1)求C的方程;
(2)设直线 与C交于A,B两点.问k为何值时
与C交于A,B两点.问k为何值时

 ?此时
?此时 的值是多少?
的值是多少?
已知数列 的前
的前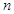 项和为
项和为 ,对一切正整数
,对一切正整数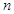 ,点
,点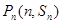 都在函数
都在函数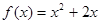 的图象上.
的图象上.
(1)求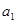 ,
, ;
;
(2)求数列 的通项公式;
的通项公式;
(3)若 ,求证数列
,求证数列 的前
的前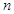 项和
项和 .
.