已知数列 的前
的前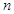 项和为
项和为 ,对一切正整数
,对一切正整数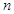 ,点
,点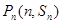 都在函数
都在函数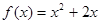 的图象上.
的图象上.
(1)求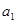 ,
, ;
;
(2)求数列 的通项公式;
的通项公式;
(3)若 ,求证数列
,求证数列 的前
的前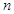 项和
项和 .
.
已知函数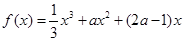 。
。
(1)若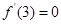 ,求a的值;
,求a的值;
(2)若a>1,求函数f(x)的单调区间与极值点;
(3)设函数 是偶函数,若过点A(1,m)
是偶函数,若过点A(1,m)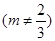 可作曲线y=f(x)的三条切线,求实数m的范围。
可作曲线y=f(x)的三条切线,求实数m的范围。
已知椭圆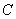 :
: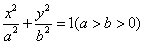 的一个顶点为
的一个顶点为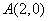 ,离心率为
,离心率为 .直线
.直线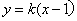 与椭圆
与椭圆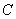 交于不同的两点M,N.
交于不同的两点M,N.
(Ⅰ)求椭圆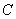 的方程;
的方程;
(Ⅱ)当△AMN得面积为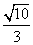 时,求
时,求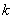 的值.
的值.
已知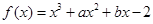 的图象过点
的图象过点 ,且函数
,且函数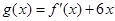 的图象关于
的图象关于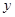 轴对称;
轴对称;
(1)求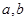 的值及函数
的值及函数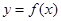 的单调区间;
的单调区间;
(2)求函数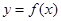 极值.
极值.
某工厂生产一种产品,已知该产品的月产量x吨与每吨产品的价格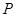 (元)之间的关系为
(元)之间的关系为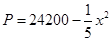 ,且生产
,且生产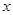 吨的成本为
吨的成本为 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
已知椭圆的顶点与双曲线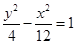 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为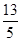 ,若椭圆的焦点在
,若椭圆的焦点在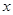 轴上,求椭圆的方程.
轴上,求椭圆的方程.