已知函数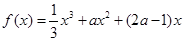 。
。
(1)若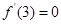 ,求a的值;
,求a的值;
(2)若a>1,求函数f(x)的单调区间与极值点;
(3)设函数 是偶函数,若过点A(1,m)
是偶函数,若过点A(1,m)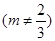 可作曲线y=f(x)的三条切线,求实数m的范围。
可作曲线y=f(x)的三条切线,求实数m的范围。
(本题满分16分)A、B是函数f(x)= +
+ 的图象上的任意两点,且
的图象上的任意两点,且 =
= (
( ),已知点M的横坐标为
),已知点M的横坐标为 .
.
(Ⅰ)求证:M点的纵坐标为定值;
(Ⅱ)若Sn=f( )+f(
)+f( )+…+f(
)+…+f( ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn;
(Ⅲ)已知数列{an}的通项公式为 . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn< (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数 的取值范围.
的取值范围.
(文科)(本题满分14分)设函数f(x)= ·
· ,其中
,其中 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点(
=(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点( ,2).
,2).
(Ⅰ)求实数m的值;
(Ⅱ)求函数f(x)的最小值及此时x值的集合
(理科)(本题满分14分)已 知函数f(x)=ex-kx,x∈R
知函数f(x)=ex-kx,x∈R
(Ⅰ)若k=e,试确定函数f(x)的单调区间
(Ⅱ)若k>0,且对于任意x∈R,f(|x|)>0恒成立,试确定实数k的取值范围
(本题满分14分)数列{an}中,a1=2,an+1=an+cn(c是常数,n=1,2,3,…),且a1,a2,a3成公比不为1的等比数列
(Ⅰ)求c的值
(Ⅱ)求{an}的通项公式
(本题满分14分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}
(Ⅰ)若A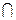 B=[0,3],求实数m的值
B=[0,3],求实数m的值
(Ⅱ)若A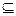 CRB,求实数m的取值范围
CRB,求实数m的取值范围
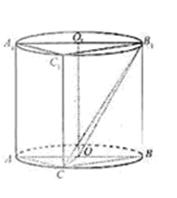
( 12分)如图,圆柱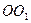 内有一个三棱柱
内有一个三棱柱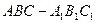 ,三棱柱的底面为圆柱底面的内接三角形,且
,三棱柱的底面为圆柱底面的内接三角形,且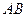 是圆
是圆 的直径。
的直径。
(1)求证:平面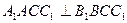
(2)设 ,在圆柱
,在圆柱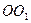 内随机选取一个点,记该点取自三棱
内随机选取一个点,记该点取自三棱
柱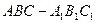 的概率为
的概率为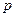
(i)当点C在圆周上运动时,求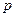 的最大值;
的最大值;
(ii)记平面 与平面
与平面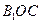 所成的角为
所成的角为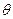
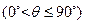 ,当
,当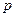
取最大值时,求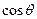 的值。
的值。