(文科)(本题满分14分)设函数f(x)= ·
· ,其中
,其中 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点(
=(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点( ,2).
,2).
(Ⅰ)求实数m的值;
(Ⅱ)求函数f(x)的最小值及此时x值的集合
(理科)(本题满分14分)已 知函数f(x)=ex-kx,x∈R
知函数f(x)=ex-kx,x∈R
(Ⅰ)若k=e,试确定函数f(x)的单调区间
(Ⅱ)若k>0,且对于任意x∈R,f(|x|)>0恒成立,试确定实数k的取值范围
如图,已知 , 四边形
, 四边形 是梯形,
是梯形, ∥
∥ ,
,  ,
, ,
, 

 中
中 点。
点。
(1)求证: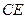 ∥平面
∥平面 ;
;
(2)求异面直线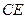 与
与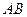 所成角的余弦值。
所成角的余弦值。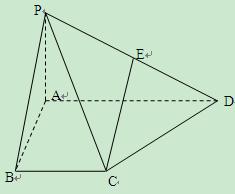
设 ,解关于
,解关于 的不等式
的不等式 。
。
围建一个面积为360㎡的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其它三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出 口,如图所示。已知旧墙的维修费用为45元/m ,新墙的造价为180元/m ,设利用的旧墙的长度为
口,如图所示。已知旧墙的维修费用为45元/m ,新墙的造价为180元/m ,设利用的旧墙的长度为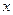 (单位:m), 修建此矩形场地围墙的总费用为
(单位:m), 修建此矩形场地围墙的总费用为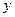 (单位:元)。
(单位:元)。
(1)将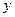 表示为
表示为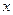 的函数;
的函数;
(2)试确定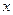 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
已知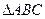 的内角
的内角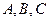 所对的边分别为
所对的边分别为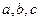 ,且
,且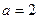 ,
,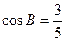 ,
,
(1)若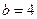 ,求
,求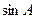 的值;
的值;
(2)若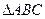 的面积
的面积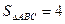 , 求
, 求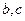 的值。
的值。
记等比数列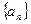 的前
的前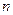 项和为
项和为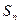 ,已知
,已知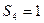 ,
,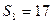 , 求数列
, 求数列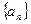 的通项公式。
的通项公式。