(本小题满分12分)
已知直线l1:4x:-3y+6=0和直线l2:x=- ,.若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
,.若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(I )求抛物线C的方程;
(II)直线l过抛物线C的焦点F与抛物线交于A,B两点,且AA1,BB1都垂直于直线l2,垂足为A1,B1,直线l2与y轴的交点为Q,求证: 为定值。
为定值。
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线M的参数方程为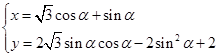
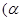 为参数),若以直角坐标系中的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为
为参数),若以直角坐标系中的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为 (t为参数).
(t为参数).
(Ⅰ)求曲线M和N的直角坐标方程,
(Ⅱ)若曲线N与曲线M有公共点,求t的取值范围.
(本小题满分10分)选修4--1:几何证明选讲
如图,已知圆O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是圆O的直径.过点C作圆O的切线交BA的延长线于点F.
(Ⅰ)求证:AC·BC=AD·AE;
(Ⅱ)若AF=2, CF=2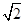 ,求AE的长.
,求AE的长.
(本小题满分12分)已知函数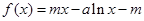 ,
, ,其中
,其中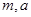 均为实数.
均为实数.
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)设 ,
, ,若对任意的
,若对任意的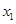 、
、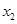
 ,
,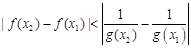 恒成立,求实数
恒成立,求实数 的最小值;
的最小值;
(本小题满分12分)已知抛物线
 的焦点为
的焦点为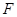 ,抛物线上存在一点
,抛物线上存在一点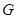 到焦点的距离为
到焦点的距离为 ,且点
,且点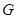 在圆
在圆
 上.
上.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)已知椭圆
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且离心率为
的焦点重合,且离心率为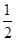 .直线
.直线 交椭圆
交椭圆 于
于 、
、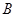 两个不同的点,若原点
两个不同的点,若原点 在以线段
在以线段 为直径的圆的外部,求
为直径的圆的外部,求 的取值范围.
的取值范围.
(本小题满分12分)如图,四棱锥 中,底面四边形
中,底面四边形 为直角梯形,对角线
为直角梯形,对角线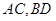 交与点
交与点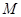 ,
, ,
, 底面
底面 ,点
,点 为棱
为棱 上一动点。
上一动点。
(Ⅰ)证明: ;
;
(Ⅱ)若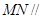 平面
平面 ,求三棱锥
,求三棱锥 的体积.
的体积.