如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是 上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.
上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.
(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.
如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围。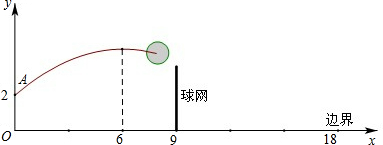
如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等,设BC=a、AC=b、AB=c.
(1)求线段BG的长;
(2)求证:DG平分∠EDF;
(3)连接CG,如图2,若△BDG与△DFG相似,求证:BG⊥CG.
甲、乙两家商场进行促销活动,甲商场采用“慢200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元;……,乙商场按顾客购买商品的总金额打6折促销。
(1)若顾客在甲商场购买了510元的商品,付款时应付多少钱?
(2)若顾客在甲商场购买商品的总金额为x(400≤x<600)元,优惠后得到商家的优惠率为p(p= ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(200≤x<400)元,你认为选择哪家商场购买商品花钱较少?请说明理由。
九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,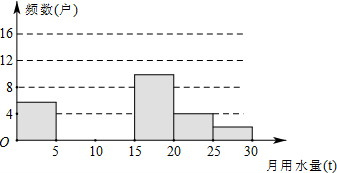
月均用水量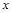 (t) (t) |
频数(户) |
频率 |
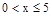 |
6 |
0.12 |
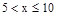 |
0.24 |
|
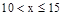 |
16 |
0.32 |
 |
10 |
0.20 |
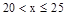 |
4 |
|
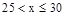 |
2 |
0.04 |
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
如图,在△ABC中,∠A=30°,∠B=45°,AC= ,求AB的长,
,求AB的长,