如图所示,在直角坐标系xOy内,有一质量为m,电荷量为+q的粒子A从原点O沿y 轴正方向以初速度V0射出,粒子重力忽略不计,现要求该粒子能通过点P(a, -b),可通 过在粒子运动的空间范围内加适当的“场”来实现。
(1) 若只在整个I、II象限内加垂直纸面向外的匀强磁场,使粒子A在磁场中作匀速 圆周运动,并能到达P点,求磁感应强度B的大小;
(2) 若只在x轴上某点固定一带负电的点电荷 Q,使粒子A在Q产生的电场中作匀速圆周运动,并能到达P点,求点电荷Q的电量大小;
(3) 若在整个I、II象限内加垂直纸面向外的 匀强磁场,并在第IV象限内加平行于x轴,沿x轴 正方向的匀强电场,也能使粒子A运动到达P点。如果此过程中粒子A在电、磁场中运动的时间相等,求磁感应强度B的大小和电场强度E的大小
如图所示,质量为m1=5 kg的物体,置于一粗糙的斜面上,用一平行于斜面的大小为30 N的力F推物体,物体沿斜面向上匀速运动,斜面体质量m2=10 kg,且始终静止,取g=10 m/s2,求:
(1)斜面对滑块的摩擦力;
(2)地面对斜面体的摩擦力和支持力.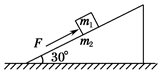
火车正常行驶的速度是54km/h,关闭发动机后,开始做匀减速运动,6s末的速度是43.2km/h,求:
(1)火车的加速度大小
(2)15s末的速度大小
(3)45s末的速度大小
如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O。轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=370,物体甲、乙均处于静止状态。(已知:sin370=0.6,cos370=0.8,设最大静摩擦力等于滑动摩擦力)求: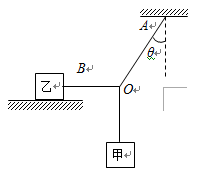
(1)轻绳OA、OB受到的拉力各为多大?
(2)若物体乙的质量m2=4kg,物体乙与水平面之间的动摩擦因数为μ=0.3,则欲使物体乙在水平面上不滑动,物体甲的质量m1最大不能超过多少?
一辆汽车初速度为10m/s,以2m/s2的加速度加速行驶,求:
(1)汽车在6s末的速度为多少?
(2)汽车在6s内前进的位移为多少?
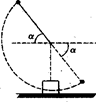
如图所示,摆锤质量为M,摆杆长为L,杆质量不计,摆杆初始位置与水平面成α,释放后摆锤绕O轴做圆周运动,在最低点与质量为m的铁块(可视为质点)相碰后又上升到图中虚线位置,若铁块与水平面间的动摩擦因数为μ,求碰后钢铁块能滑行的距离?