如图所示，一个半径为R、内侧光滑的圆形轨道平放于光滑水平面上并被固定，其圆心为O。有a、b两个可视为质点的小球，分别静止靠在轨道内侧、直径AB的两端，两球质量分别为ma =" 4" m和mb = m。现给a球一个沿轨道切线方向的水平初速度v0，使其从A向B运动并与b球发生弹性碰撞，已知两球碰撞时间极短，求两球第一次碰撞和第二次碰撞之间的时间间隔。
一质量m＝0.5kg的滑块以一定的初速度冲上一倾角为30º足够长的斜面，某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度，如图所示为通过计算机绘制出的滑块上滑过程的v－t图。求：（g取10m/s2）
（1）滑块与斜面间的动摩擦因数；
（2）判断滑块最后能否返回斜面底端？若能返回，求出返回斜面底端时的动能；若不能返回，求出滑块停在什么位置。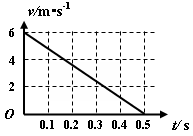
如图所示，半径R=0.9m的光滑的半圆轨道固定在竖直平面内，直径AC竖直，下端A与光滑的水平轨道相切。一小球沿水平轨道进入竖直圆轨道，通过最高点C时对轨道的压力为其重力的3倍。不计空气阻力，g取10m/s2。求：
（1）小球在A点的速度大小；
（2）小球的落地点到A点的距离。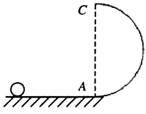
如图所示，质量为1kg的小物块以5m/s的初速度滑上一块原来静止在水平面上的木板，木板质量为4kg，木板与水平面间的动摩擦因数为0.02，经时间2s后，小物块从木板另一端以1m/s相对于地的速度滑出，g=10m/s2，求这一过程中木板的位移和系统在此过程中因摩擦增加的内能.
两个氘核发生了如下核反应：
，其中氘核质量为2.1036u，氢核质量为3.1050u，中子质量为1.0087u。求：
①核反应中释放的核能。
②在两个氘核以相等的动能0.35MeV进行对心碰撞，并且核能全部转化为机械能的情况下，求反应中产生的中子和氦核的动能。
③假设反应中产生的氦核沿直线向原来静止的碳核(
C)接近，受库仑力的影响，当它
们的距离最近时，两个原子核的
动能各是多少?
氢原子在某三个相邻能级之间跃迁时，可能发出三种不同波长的辐
射光。已知其中的两个波长分别为
和
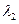，且>。
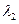求：另一个波长可能是多少？