(本小题满分12分)
已知向量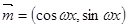 ,
, ,设函数
,设函数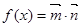 .
.
(Ⅰ)若函数 的零点组成公差为
的零点组成公差为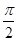 的等差数列,求函数
的等差数列,求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数 的图象的一条对称轴是
的图象的一条对称轴是 ,(
,(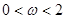 ),求函数
),求函数 的值域.
的值域.
定义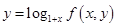 ,
,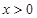 ,
,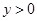 .
.
(1)比较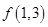 与
与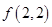 的大小;
的大小;
(2)若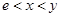 ,证明:
,证明: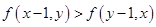 ;
;
(3)设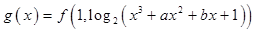 的图象为曲线
的图象为曲线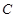 ,曲线
,曲线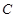 在
在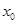 处的切线斜率为
处的切线斜率为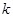 ,若
,若 ,且存在实数
,且存在实数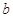 ,使得
,使得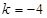 ,求实数
,求实数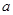 的取值范围.
的取值范围.
某营养师要为某个儿童预订午餐和晚餐,已知一个单位的午餐含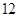 个单位的碳水化合物,
个单位的碳水化合物,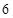 个单位的蛋白质和
个单位的蛋白质和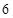 个单位的维生素
个单位的维生素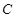 ;一个单位的晚餐含
;一个单位的晚餐含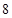 个单位的碳水化合物,
个单位的碳水化合物,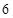 个单位的蛋白质和
个单位的蛋白质和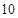 个单位的维生素
个单位的维生素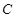 .另外,该儿童这两餐需要的营养中至少含
.另外,该儿童这两餐需要的营养中至少含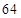 个单位的碳水化合物,
个单位的碳水化合物,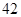 个单位的蛋白质和
个单位的蛋白质和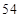 个单位的维生素
个单位的维生素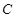 .如果一个单位的午餐、晚餐的费用分别是
.如果一个单位的午餐、晚餐的费用分别是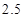 元和
元和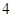 元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
设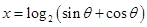 ,
,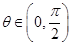 .
.
(1)求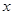 的取值范围;
的取值范围;
(2)设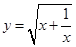 ,试问当
,试问当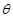 变化时,
变化时,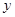 有没有最小值,如果有,求出这个最小值,如果没有,说明理由.
有没有最小值,如果有,求出这个最小值,如果没有,说明理由.
如图,在三棱锥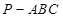 中,
中,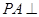 平面
平面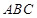 ,
,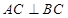 ,
,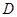 为侧棱
为侧棱 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.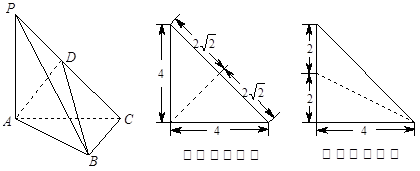
(1)证明: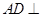 平面
平面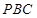 ;
;
(2)在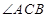 的平分线上确定一点
的平分线上确定一点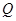 ,使得
,使得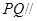 平面
平面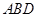 ,并求此时
,并求此时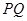 的长.
的长.
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔 小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.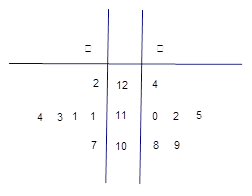
(1)根据样品数据,计算甲、乙两个车间产品重量的平均值与方差,并说明哪个车间的产品的重量相对较稳定;
(2)若从乙车间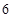 件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过
件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过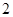 克的概率.
克的概率.