某汽车在刹车后行驶的距离s(单位:m)与时间t(单位:s)之间的关系得部分数据如下表:
| 时间t(s) |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
1.2 |
… |
| 行驶距离s(m) |
0 |
2.8 |
5.2 |
7.2 |
8.8 |
10 |
10.8 |
… |
假设这种变化规律一直延续到汽车停止.
(1)根据这些数据在给出的坐标系中画出相应的点;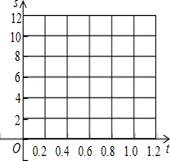
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)刹车后汽车行驶了多长距离才停止?
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,求∠2的度数.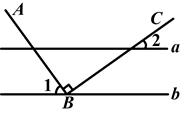
如图,D,E,F是线段AB的四等分点.
(1)过点D作DH∥BC交AC于H,过点E作EG∥BC交AC于点G,过点F作FM∥BC交AC于M;
(2)量出线段CH,HG,GM,MA的长度,你有什么发现;
(3)量出线段HD,EG,FM,BC的长度后,你又有什么发现.
如图,在梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.
(1)PQ与BC平行吗?为什么?
(2)测量DQ与CQ的长,DQ与CQ是否相等?
(3)测量PQ、AD和BC的长度,你会发现PQ与AD+BC有什么数量关系?
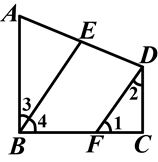
如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°.试说明AB∥EF.
如图,AB⊥BC,∠1+∠2=90°,∠2=∠3.BE与DF平行吗?为什么?