在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线， DE⊥AB于点E．
（1）如图1，连接EC，求证：△EBC是等边三角形；
（2）点M是线段CD上的一点（不与点C，D重合），以BM为一边，在BM的下方作∠BMG=60°，MG交DE延长线于点G．请你在图2中画出完整图形，并直接写出MD，DG与AD之间的数量关系；
（3）如图3,点N是线段AD上的一点，以BN为一边，在BN的下方作∠BNG=60°，NG交DE延长线于点G，且MB=MG．试探究ND，DG与AD数量之间的关系，并说明理由．
如图①所示是一个长为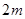
，宽为
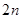的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形．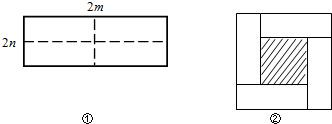
（1）你认为图②中的阴影部分的正方形的边长等于；
（2）请用两种不同的方法列代数式表示图②中阴影部分的面积．
方法① ．方法② ；
（3）观察图②，你能写出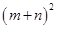
，
，
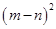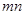这三个代数式之间的等量关系吗？
答：.
（4）根据（3）题中的等量关系，解决如下问题：若
，
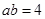，则求
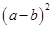的值．
（1）写出一个含有字母x的代数式，当x =1时，代数式的值等于2；
（2）写出一个含有字母x的代数式，当x =4和x =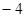
时，代数式的值都等于5；
（3）写出两个只含有字母x的二次三项式，当x不论取什么值时，这两个多项式的和总是等于3（列式表示）．
某型号汽车油箱的最大贮油量为60L，在正常情况下，每行驶50km耗油5.5L．
（1）在加满油的情况下，该车正常行驶x km后，油箱内还剩的油量是多少？
（2）试通过计算判断，在加满油的情况下，若该车要正常行驶到550km外的某地，中途是否需要再加油？
如图，是由若干个完全相同的小正方体组成的一个几何体．
（1）请画出这个几何体的三视图；
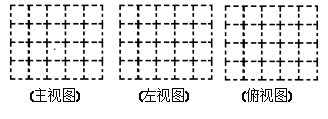
（2）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的主视图和俯视图不变，那么最多可以再添加______个小正方体.
邮递员骑车从邮局出发，先向西骑行3km到达A村，继续向西骑行２km到达B村，然后向东骑行7km到达C村，再继续向东骑行3km到达D村，最后骑回邮局．
（1）C村离A村有多远？
（2）邮递员一共骑行了多少千米？