如图①所示是一个长为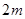 ,宽为
,宽为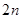 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.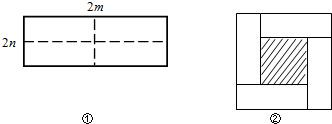
(1)你认为图②中的阴影部分的正方形的边长等于 ;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① .方法② ;
(3)观察图②,你能写出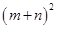 ,
,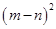 ,
,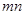 这三个代数式之间的等量关系吗?
这三个代数式之间的等量关系吗?
答: .
(4)根据(3)题中的等量关系,解决如下问题:若 ,
,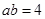 ,则求
,则求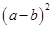 的值.
的值.
(1)先求解下列两题:
①如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数;
②如图②,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数 (x>0)的图象经过点B,D,求k的值.
(x>0)的图象经过点B,D,求k的值.
(2)解题后,你发现以上两小题有什么共同点?请简单地写出.
如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连结BE.请找出一对全等三角形,并说明理由.
如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1S2+S3(用“>”、“=”、“<”填空);
(2)写出如图中的三对相似三角形,并选择其中一对进行证明.
阅读材料:求1+2+22+23+24+…+22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22013+22014
将下式减去上式得2S-S=22014-1
即S=22014-1
即1+2+22+23+24+…+22013=22014-1
请你仿照此法计算:
(1)1+2+22+23+24+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数).
如图,矩形ABCD中,AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,第n次平移将矩形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向平移5个单位,得到矩形AnBnCnDn(n>2).
(1)求AB1和AB2的长.
(2)若ABn的长为56,求n.