一质量为m=2kg的小滑块，从半径R=1.25m的
光滑圆弧轨道上的A点由静止滑下，圆弧轨道竖直固定，其末端B切线水平。a、b两轮半径r=0.4m，滑块与传送带间的动摩擦因数µ=0.1，传送带右端点C距水平地面的高度h=1.25m，E为C的竖直投影点。g取10m/s2，求：
（1）当传送带静止时，滑块恰能在b轮最高点C离开传送带，则BC两点间的距离是多少？
（2）当a、b两轮以某一角速度顺时针转动时，滑块从C点飞出落到地面D点，已知CD两点水平距离为3m。试求：a、b两轮转动的角速度和滑块与传送带间产生的内能。
用轻绳AC和BC悬挂一重物，绳AC和BC与水平天花板的夹角分别为600和300，如图所示，已知悬挂重物的重力100N，求AC绳和BC绳产生的拉力？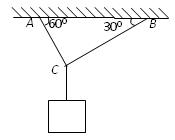
如图所示，一个重为100N的小球被夹在竖直的墙壁和A点之间，已知球心O与A点的连线与竖直方向成
角，且=370，所有接触点和面均不计摩擦。试求小球对墙面的压力F1和对A点压力F2(sin370=0.6；cos370=0.8；tan370=0.75，要求作图）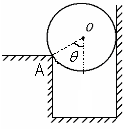
如图所示，在一条小河中有一条小船，船受到一个与河岸成30°角的拉力F="1000" N的作用．若要使船沿与河岸平行的方向前进，需要另加一个力的作用，则这个力向什么方向加可以最省力？该力的大小为多少？（要求作图）
有某校一课外活动小组自制一枚火箭，设火箭发射后始终在垂直于地面的方向上运动．火箭点火后可认为做匀加速直线运动，经过4 s到达离地面40 m高处时燃料恰好用完，若不计空气阻力，取g＝10 m/s2，求：燃料恰好用完时火箭的速度
火箭上升离地面的最大高度
飞机着陆后匀减速滑行，它滑行的初速度是60m/s，加速度大小是3m/s2,则：飞机着陆后滑行的时间是多少？
要滑行多远才能停下来？