(本小题满分12分)设直线 与椭圆
与椭圆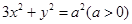 相交于
相交于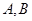 两个不同的点,与
两个不同的点,与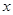 轴相交于点
轴相交于点 ,记
,记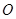 为坐标原点.
为坐标原点.
(1)证明: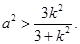
(2)若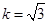 且
且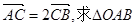 的面积及椭圆方程.
的面积及椭圆方程.
(本小题满分14分)椭圆 ,椭圆的左、右焦点分别为
,椭圆的左、右焦点分别为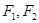 ,椭圆上的点到中心的最短距离为
,椭圆上的点到中心的最短距离为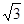 ,且椭圆上的点到左焦点
,且椭圆上的点到左焦点 的最长距离为
的最长距离为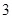 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若直线 交
交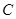 于A,B两点.若AB的中点坐标的纵坐标为
于A,B两点.若AB的中点坐标的纵坐标为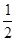 ,求
,求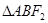 的面积.
的面积.
(本小题满分13分)已知函数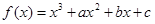 (其中,
(其中,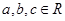 ),
),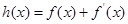 为奇函数,
为奇函数,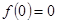 .
.
(Ⅰ)求函数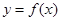 的解析式;
的解析式;
(Ⅱ)求函数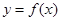 在
在 上的最值.
上的最值.
(本小题满分12分)已知数列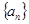 中,
中,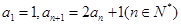 .
.
(Ⅰ)求证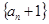 是等比数列,并求
是等比数列,并求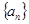 的通项公式;
的通项公式;
(Ⅱ)设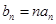 ,求数列
,求数列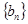 的前
的前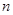 项和.
项和.
(本小题满分12分)如图,在矩形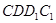 中,
中,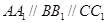 ,
,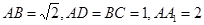 ,将在矩形
,将在矩形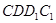 沿
沿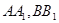 分别将四边形
分别将四边形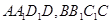 折起,使
折起,使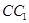 与
与 重合(如图所示)
重合(如图所示)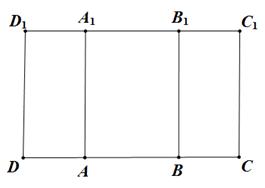
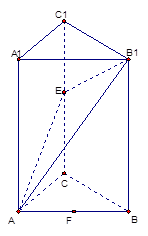
(Ⅰ)在三棱柱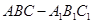 中,取
中,取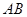 的中点
的中点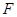 ,求证:
,求证: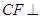 平面
平面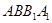 ;
;
(Ⅱ)当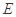 为棱
为棱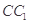 中点时,求证:
中点时,求证: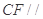 平面
平面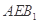 .
.
(本小题满分12分)《中国足球改革发展总体方案》明确指出:加强对国家队经费投入、奖励政策、基地建设、后勤服务、情报信息等方面的保障,提高服务水平。新建2个国家足球训练基地,满足国家队不同季节的比赛和训练需要。有关机构分别对甲、乙两个地区的7个城市进行评估量化,它们的量化分数的茎叶图如图所示,其中甲地区城市的平均量化分为85,乙地区城市的中位数为83.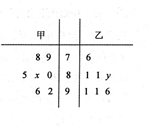
(Ⅰ)求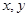 的值;
的值;
(Ⅱ)从量化分在90分以上的城市中随机抽取两个城市,求乙地区至少有一个城市的概率.