二次函数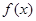 满足
满足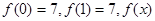 的最大值是8,
的最大值是8,
(1)求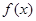 的解析式;
的解析式;
(2)在区间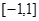 上,
上, 的图象恒在
的图象恒在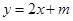 的上方,试确定
的上方,试确定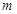 的范围。
的范围。
设P:关于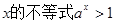 的解集是
的解集是 ,Q:函数
,Q:函数 的定义域为R,如果P,Q有且仅有一个正确,求实数
的定义域为R,如果P,Q有且仅有一个正确,求实数 的取值范围。
的取值范围。
在对人们休闲方式的一次调查中,共调查120人,其中女性70人、男性50人,女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)在犯错误的概率不超过0.10的前提下,认为休闲方式与性别是否有关?
参考数据:独立性检验临界值表
参考公式:独立性检验随机变量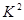 值的计算公式:
值的计算公式: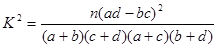 (其中
(其中 )
)
计算下列各题:
①
②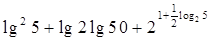
设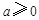 ,
,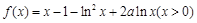 .
.
(Ⅰ)令 ,讨论
,讨论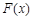 在
在 内的单调性并求极值;
内的单调性并求极值;
(Ⅱ)当 时,试判断
时,试判断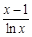 与
与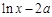 的大小.
的大小.