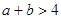扬州某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为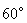 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为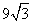 平方米,且高度不低于
平方米,且高度不低于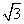 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为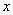 (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段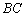 与两腰长的和)为
与两腰长的和)为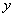 (米).
(米).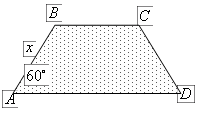
⑴求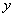 关于
关于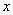 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
⑵要使防洪堤横断面的外周长不超过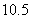 米,则其腰长
米,则其腰长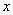 应在什么范围内?
应在什么范围内?
⑶当防洪堤的腰长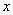 为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值
为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值
(本小题满分14分)已知命题p:方程x2+mx+1=0有两个不相等的实根;q:不等式4x2+4(m–2)x+1>0的解集为R.
(1)若命题q为真,求实数m的取值范围.
(2)若命题“p且q”和“非p”为假,求实数m的取值范围
设正项数列{an}(n≥5)对任意正整数k(k≥3)恒满足: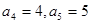 ,且
,且 .
.
(1)求数列{an}的通项公式;
(2)是否存在整数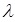 ,使得
,使得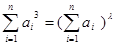 对于任意正整数n恒成立?若存在,求出
对于任意正整数n恒成立?若存在,求出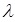 的值;若不存在,说明理由。(注:
的值;若不存在,说明理由。(注: )
)
一个正方形花圃,被分为n( )份,种植红、黄、蓝、绿4种颜色不同的花,要求相邻两部分种植不同颜色的花。
)份,种植红、黄、蓝、绿4种颜色不同的花,要求相邻两部分种植不同颜色的花。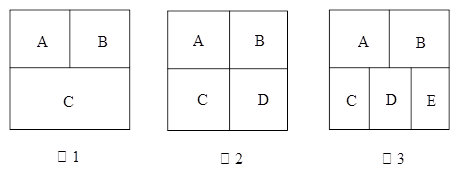
(1)如图1,正方形被分为3份A、B、C,有多少种不同的种植方法?
(2)如图2,正方形被分为4份A、B、C、D,有多少种不同的种植方法?
(3)如图3,正方形被分为5份A、B、C、D、E,有多少种不同的种植方法?
已知二次函数f(x)=ax2+bx+c .
(1)设集合A={x|f(x)=x}.
①若A={1,2},且f(0)=2,求f(x)的解析式;
②若A={1},且a≥1,求f(x)在区间[﹣2,2]上的最大值M(a).
(2)设f(x)的图像与x轴有两个不同的交点,a>0, f(c)=0,且当0<x<c时,f(x)>0.用反证法证明: .
.
(1)用分析法证明:当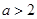 时,
时,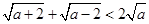 ;
;
(2)设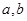 是两个不相等的正数,若
是两个不相等的正数,若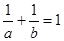 ,用综合法证明:
,用综合法证明: