如图所示，有三根长度均为L＝0.3m的不可伸长的绝缘细线，其中两根的一端分别固定在天花板上的P、Q点，另一端分别拴有质量均为m＝0.12kg的带电小球A和B，其中A球带正电，电荷量为q＝3×10－6C。A、B之间用第三根线连接起来。在水平向左的匀强电场E作用下，A、B保持静止，悬线仍处于竖直方向，且A、B间细线恰好伸直。（静电力恒量k＝9×109N·m2/ C2，取g="l0" m/s2）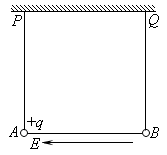 
（1）此匀强电场的电场强度E为多大；
（2）现将PA之间的线烧断，由于有空气阻力，A、B球最后会达到新的平衡位置。求此时细线QB所受的拉力T的大小，并求出A、B间细线与竖直方向的夹角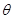
；
（3）求A球的电势能与烧断前相比改变了多少（不计B球所带电荷对匀强电场的影响）。
如图所示，质量M=2kg的滑块套在光滑的水平轨道上，质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接，小球和轻杆可在竖直平面内绕O轴自由转动，开始轻杆处于水平状态，现给小球一个竖直向上的初速度
="4" m/s，g取10
。
（1）若锁定滑块，试求小球通过最高点P时对轻杆的作用力大小和方向。
（2）若解除对滑块的锁定，试求小球通过最高点时的速度大小。
（3）在满足（2）的条件下，试求小球击中滑块右侧轨道位置点与小球起始位置点间的距离。
欲使示波器光屏上出现一条竖直亮线，应怎样调节示波器？
当温度升高时，物体内分子的运动情况将如何变化？
在水平线上有17个质点，每相邻两个质点间距离为4cm，如图所示.有一简谐波在该水平线上传播.已知第5个质点完成一次全振动经过的路程为8cm，时间为2s，当它从平衡位置开始向上振动通过12cm的路程时，第17个质点即将振动，求：
(1)该列波的传播速度。
(2)在图中画出第17个质点即将振动时的波形图，并标出第17个质点的振动方向。
质量为m=1kg的物体与水平面间的动摩擦因数μ=0.6，在F=10N水平拉力作用下，由静止开始前进x1=2m后撤去外力， g=10m/s2,求：
（1）撤去外力时物体速度多大？
（2）撤去外力后还能运动多远？