已知两点F1(-1,0)及F2(1,0),点P在以F1、F2为焦点的椭圆C上,且|PF1|、|F1F2|、|PF2|构成等差数列.
(1)求椭圆C的方程;
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l.求四边形F1MNF2面积S的最大值.
已知动点 到定点
到定点 和
和 的距离之和为
的距离之和为 .
.
(Ⅰ)求动点 轨迹
轨迹 的方程;
的方程;
(Ⅱ)设 ,过点
,过点 作直线
作直线 ,交椭圆
,交椭圆 异于
异于 的
的 两点,直线
两点,直线 的斜率分别为
的斜率分别为 ,证明:
,证明: 为定值.
为定值.
在如图所示的几何体中,四边形 均为全等的直角梯形,且
均为全等的直角梯形,且 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)设 ,求点
,求点 到平面
到平面 的距离.
的距离.
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如下:
(Ⅰ)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(Ⅱ)若用分层抽样的方法从分数在 和
和  的学生中共抽取3人,该3人中成绩在
的学生中共抽取3人,该3人中成绩在 的有几人?
的有几人?
(Ⅲ)在(Ⅱ)中抽取的3人中,随机抽取2人,求分数在 和
和  各1人的概率.
各1人的概率.
在 中,角
中,角 所对的边分别是
所对的边分别是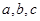 ,已知
,已知 .
.
(Ⅰ)求 ;
;
(Ⅱ)若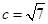 ,且
,且 ,求
,求 的面积.
的面积.
设函数 .
.
(Ⅰ)解不等式 ;
;
(Ⅱ)若不等式 的解集为
的解集为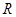 ,求实数
,求实数 的取值范围.
的取值范围.