阅读材料，解答问题：
为解方程 (x2-1)2-5(x2-1)+4=0，我们可以将x2-l看作一个整体，然后设x2-l=y，那么原方程可化为y2-5y＋4=0①，解得y1 =1，y2=4．当y1=l时， x2-l=1．所以x2 =2．所以x=±
；当y=4时，x2-1=4．所以x2 =5．所以x=±
，故原方程的解为x1=，x2=-，x3=，x4=；上述解题过程，在由原方程得到方程①的过程中，利用换元法达到了降次的目的，体现了转化的数学思想．请利用以上知识解方程：x4-x2-6＝0．
如图1，某超市从一楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2．4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，求二楼的层高BC约为多少米？（ sin42°≈0．7，tan42°≈0．9）
已知关于
的一元二次方程 
有两个不相等的实数根．
（1）求
的取值范围；
（2）若为正整数，求该方程的根．
先化简：
，再选取一个合适的a值代入计算．
（1）计算：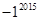
+
﹣sin45°
（2）化简：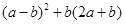
（14’）如图，在平面直角坐标系
中，A、B为
轴上两点，C、D为
轴上的两点，经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C的坐标为（0，
），点M是抛物线C2：
（
＜0）的顶点．
（1）求A、B两点的坐标；
（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；
（3）当△BDM为直角三角形时，求的值．