数学兴趣小组想测量一棵树的高度，在阳光下，一名同学测得一根长为1m的竹竿的影长为0.8m，同时另一名同学测量一棵树的高度时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上，其中，落在墙壁上的影长为1.5m，落在地面上的影长为4.8m，求树的高为多少米?
回答下列问题：
⑴如图所示的甲、乙两个平面图形能折什么几何体？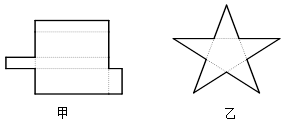
（2）由多个平面围成的几何体叫做多面体.若一个多面体的面数为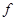
，顶点个数为
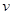，棱数为
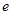，分别计算第（1）题中两个多面体的
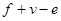的值？你发现什么规律？
（3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数.
阅读计算：
阅读下列各式：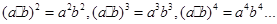
回答下列三个问题:
①验证: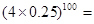 
__ .
__.
②通过上述验证， 归纳得出：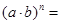
__；
__ .
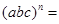请应用上述性质计算：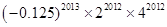
若点C在线段AB的延长线上，点D、E分别为线段CB、AC的中点，DE＝6,画出图形并求AB的长度.
如图所示，点D、E分别为线段CB、AC的中点，若ED＝6，求线段AB的长度．
（1）化简后再求值：
，其中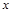
、
、
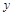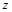满足下列方程●●●．圆点部分是被周亮不小心用墨水污染的条件，可是汤灿同学却认为不要那部分条件也能求出正确答案，你同意汤灿同学的说法吗？请你通过计算解释原因。
①你的判断是（填同意或者不同意）.
②原因：