先化简,再求值: ,其中 .
计算: .
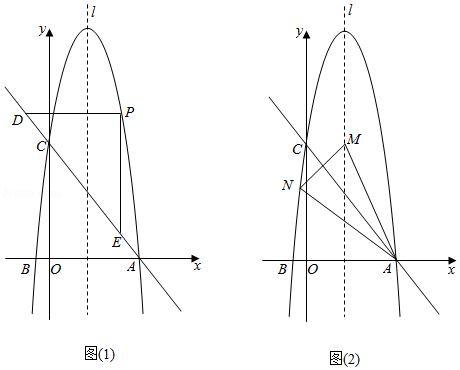
已知抛物线 交 轴于点 和点 ,交 轴于点 .
(1)求抛物线的解析式和顶点坐标;
(2)如图(1),点 是抛物线上位于直线 上方的动点,过点 分别作 轴、 轴的平行线,交直线 于点 , ,当 取最大值时,求点 的坐标;
(3)如图(2),点 为抛物线对称轴 上一点,点 为抛物线上一点,当直线 垂直平分 的边 时,求点 的坐标.
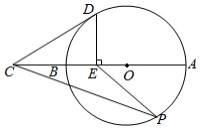
古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图,线段 是 的直径,延长 至点 ,使 ,点 是线段 的中点, 交 于点 ,点 是 上一动点(不与点 , 重合),连接 , , .
(1)求证: 是 的切线;
(2)小明在研究的过程中发现 是一个确定的值.回答这个确定的值是多少?并对小明发现的结论加以证明.
随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的 型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少 ,求:
(1) 型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批 型车和新款 型车共60辆,且 型车的进货数量不超过 型车数量的两倍.已知 型车和 型车的进货价格分别为1500元和1800元,计划 型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?