(本小题满分l2分)
如图,在多面体ABCDEF中,ABCD为菱形, ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA 面ABCD,G为BF的中点,若EG//面ABCD.
面ABCD,G为BF的中点,若EG//面ABCD.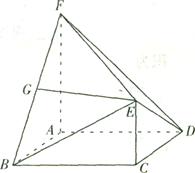
(1)求证:EG 面ABF;
面ABF;
(2)若AF=AB,求二面角B—EF—D的余弦值.
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点记忆三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量
(单位:
)与它的"相近"作物株数
之间的关系如下表所示:
| 1 |
2 |
3 |
4 |
|
| 51 |
48 |
45 |
42 |
这里,两株作物"相近"是指它们之间的直线距离不超过1米.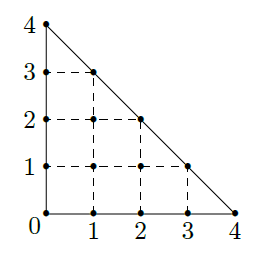
(I)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好"相近"的概率;
(II)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.
已知函数
.
(I)若
是第一象限角,且
.求
的值;
(II)求使
成立的
的取值集合.
设函数
(其中
).
(Ⅰ) 当
时,求函数
的单调区间;
(Ⅱ) 当
时,求函数
在
上的最大值
.
已知抛物线
的顶点为原点,其焦点
到直线
的距离为
.设
为直线
上的点,过点
作抛物线
的两条切线
,其中
为切点
(Ⅰ) 求抛物线
的方程;
(Ⅱ) 当点
为直线 上的定点时,求直线
的方程;
上的定点时,求直线
的方程;
(Ⅲ) 当点
在直线
上移动时,求
的最小值.
设数列
的前
项和为
.已知
.
(Ⅰ) 求
的值;
(Ⅱ) 求数列
的通项公式;
(Ⅲ) 证明:对一切正整数
,有
.