(本小题满分10分)
已知向量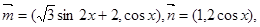 设函数
设函数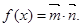
(1)求 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在△ABC中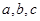 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若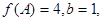 △ABC的面积为
△ABC的面积为 ,求
,求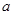 的值.
的值.
(本小题14分)已知椭圆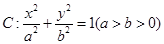 的离心率为
的离心率为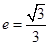 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线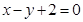 相切,
相切,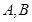 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点,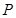 为椭圆
为椭圆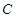 上的动点.
上的动点.
(1)求椭圆的标准方程;
(2)若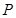 与
与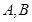 均不重合,设直线
均不重合,设直线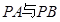 的斜率分别为
的斜率分别为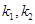 ,求
,求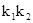 的值。
的值。
惠州市在每年的春节后,市政府都会发动公务员参与到植树活动中去.林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出的高度如下(单位:厘米)
甲:37,21,31,20,29,19,32,23,25,33
乙:10,30,47,27,46,14,26,10,44,46
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为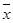 ,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入如图程序框图进行运算,问输出的S大小为多少?并说明S的统计学意义.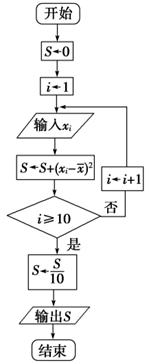
一个口袋内装有大小相同的6个小球,其中2个红球,记为A1、A2,4个黑球,记为B1、B2、B3、B4,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出的两个球颜色不同的概率.
(本题满分12分) 为了了解某中学学生的体能情况,体育组决定抽样三个年级部分学生进行跳绳测试,并将所得的数据整理后画出频率分布直方图(如图5).已知图中从左到右的前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数是5.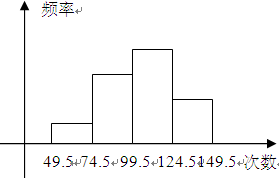
(1) 求第四小组的频率和参加这次测试的学生人数;
(2) 在这次测试中,学生跳绳次数的中位数落在第几小组内?
(3) 参加这次测试跳绳次数在100次以上为优秀,试估计该校此年级跳绳成绩的优秀率是多少?
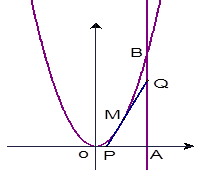
如图,由y=0,x=8,y=x2围成的曲边三角形,在曲线弧OB上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围成的三角形PQA面积最大。