已知直线 和
和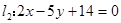 的相交于点P。
的相交于点P。
求:(Ⅰ)过点P且平行于直线 的直线方程;
的直线方程;
(Ⅱ)过点P且垂直于直线 的直线方程。
的直线方程。
(本小题满分12分)在△ABC中,a、b、c分别为角A、B、C的对边, .
.
(1)求角C;
(2)若边c=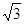 ,a+b=3,求边a和b的值.
,a+b=3,求边a和b的值.
(本小题满分12分)f(x)=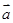 .
. ,其中向量
,其中向量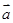 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),
=(1+sin2x,1), ,且函数
,且函数 的图象经过点
的图象经过点 .
.
(Ⅰ)求实数 的值.
的值.
(Ⅱ)求函数 的最小值及此时
的最小值及此时 值的集合.
值的集合.
(本小题满分12分)已知等比数列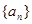 中,
中,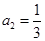 ,公比
,公比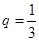 ,
,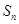 为
为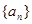 的前
的前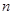 项和.
项和.
(1)求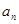 和Sn
和Sn
(2)设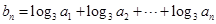 ,求数列
,求数列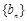 的通项公式.
的通项公式.
.选修4-5:不等式选讲
已知a,b,c∈R+,求证:
(1)(ab+a+b+1)(ab+ac+bc+c2)≥16abc;
(2)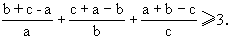
选修4-4:极坐标与参数方程
在直角坐标系xOy中,圆C1:x2+y2=4,圆C2:(x-2)2+y2=4.
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆C1,C2的极坐标方程,并求出圆C1,C2交点的极坐标;
(Ⅱ)求圆C1与C2的公共弦的参数方程.