一辆汽车在0时刻从静止开始匀加速开出,然后保持匀速运动,最后匀减速运动,直到停止,下表给出了某些时刻汽车的速度:
| 时刻/s |
1.0 |
2.0 |
3.0 |
5.0 |
7.0 |
9.5 |
10.5 |
| 速度/ m·s-1 |
3 |
6 |
9 |
12 |
12 |
9 |
3 |
(1)汽车做匀加速运动时的加速度和匀减速运动时的加速度大小分别是多少?
(2)汽车从开出到停止共经历的时间是多少?
(3)画出汽车运动全过程的v—t图像(标明相关数据)
(4)汽车通过的总路程是多少?
如图所示,一细线的一端固定于倾角为 的光滑楔形滑块A上的顶端O处,细线另一端栓一质量为
的光滑楔形滑块A上的顶端O处,细线另一端栓一质量为 的小球,取
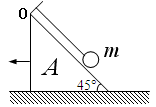
的小球,取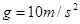 .
.
(1)当滑块静止时,线中拉力 等于多少?
等于多少?
(2)当滑块从静止向左加速运动时,小球恰好对斜面无压力,经过2秒钟小球运动的位移是多少?
如图直流电源的路端电压U=182 V,金属板AB、CD、EF、GH相互平行、彼此靠近。它们分别和变阻器上触点a、b、c、d连接。ab、bc、cd段电阻之比为1∶2∶3。孔O1正对B和E,孔O2正对D和G,边缘F、H正对。一个电子以初速度 m/s沿AB方向从A点进入电场,恰好穿过孔O1和O2后,从H点离开电场。金属板间的距离L1=2 cm,L2=4 cm,L3=6 cm。电子质量
m/s沿AB方向从A点进入电场,恰好穿过孔O1和O2后,从H点离开电场。金属板间的距离L1=2 cm,L2=4 cm,L3=6 cm。电子质量 kg,电荷量
kg,电荷量 C。正对的两平行板间可视为匀强电场,求:
C。正对的两平行板间可视为匀强电场,求:
(1) 各相对两板间的电场强度;
(2) 电子离开H点时的动能;
(3) 四块金属板的总长度(AB+CD+EF+GH)。
如图所示,质量为m=1 kg的滑块,放在光滑的水平平台上,平台的右端B与足够长的水平传送带相接,皮带轮的半径为R=0.5m,且以角速度ω=12 rad/s逆时针转动(传送带不打滑),先将滑块缓慢向左压缩固定在平台上的轻弹簧,然后突然释放,当滑块滑到传送带上距B端L=15m的C点时,与传送带速度大小相等,滑块与传送带之间的动摩擦因数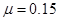 。(g="10" m/s2)求:
。(g="10" m/s2)求: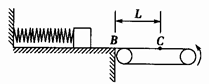
(1)释放滑块前弹簧具有的弹性势能;
(2)滑块从B到C所用的时间;
(3) 滑块从B到C系统因摩擦增加的内能。
如图所示,在绝缘水平面上,相距为L的A、B两点处分别固定着两个带电量相等的正电荷,a、b是AB连线上的两点,其中Aa=Bb=L/4,O为AB连线的中点,一质量为m带电量为+q的小滑块(可以看作质点)以初动能E 从a点出发,沿直线AB向b点运动,其中小滑块第一次经过O点时的动能为初动能的n倍(n>l),到达b点时动能恰好为零,小滑块最终停在O点,求:
从a点出发,沿直线AB向b点运动,其中小滑块第一次经过O点时的动能为初动能的n倍(n>l),到达b点时动能恰好为零,小滑块最终停在O点,求: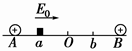
(1)小滑块与水平面间的动摩擦因数;
(2)O、b两点间的电势差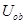 ;
;
(3)小滑块运动的总路程。
如图甲所示,两个平行金属板P、Q竖直放置,两板间加上如图乙所示的电压。t=0时,Q板比P板电势高5V,此时在两板的正中央M点有一个电子仅受电场力作用从静止开始运动,假设电子始终未与两板相碰。在0<t<8×10 10s的时间内,这个电子处于M点的右侧、速度向左且逐渐减小的时间范围是。