如图,AB是⊙O的直径,AC是弦.
(1)请你按下面步骤画图;
第一步,过点A作∠BAC的角平分线,交⊙O于点D;
第二步,过点D作AC的垂线,交AC的延长线点E.
第三步,连接BD.
(2)求证:AD2=AE•AB;
(3)连接EO,交AD于点F,若5AC=3AB,求 的值.
的值.
我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:在四边形ABCD中,取对角线BD的中点O,连接OA、OC.显然,折线AOC能平分四边形ABCD的面积,再过点O作OE∥AC交CD于E,则直线AE即为一条“好线”.
(1)试说明直线AE是“好线”的理由;
(2)如下图,AE为一条“好线”,F为AD边上的一点,请作出经过F点的“好线”,并对画图作适当说明(不需要说明理由).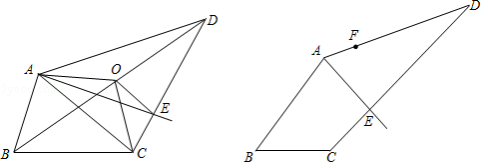
(本题6分)如图,在△ABC中,点E在BC上,CD⊥AB, EF⊥AB,垂足分别为D、F.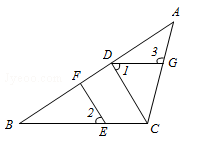
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.
一个多边形,它的内角和比外角和的5倍多180°,求这个多边形的边数及内角和度数.
先化简再求值: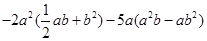 , 其中
, 其中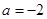 ,
,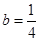 .
.
计算(每小题3分,共12分)
(1) ;
;
(2) ;
;
(3) ;
;
(4) .
.