(本小题满分10分)
在平面直角坐标系 中,直线
中,直线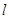 的参数方程为
的参数方程为 (t为参数,α为直线
(t为参数,α为直线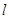 的倾斜角),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
的倾斜角),以原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 .
.
(1) 若直线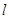 与圆C相切,求
与圆C相切,求 的值;
的值;
(2) 若 直线
直线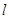 与圆C交与A,B两点,求
与圆C交与A,B两点,求 的值.
的值.
定义函数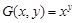 ,其中,
,其中,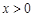 ,
, .
.
(Ⅰ)设函数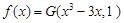 ,求
,求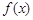 的定义域;
的定义域;
(Ⅱ)设函数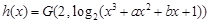 的图像为曲线
的图像为曲线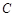 ,若存在实数
,若存在实数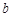 使得曲线
使得曲线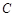 在
在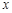
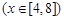 处有斜率为
处有斜率为 的切线,求实数
的切线,求实数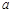 的取值范围;
的取值范围;
(Ⅲ)当 且
且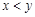 时,试比较
时,试比较 与
与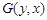 的大小(只写出结论).
的大小(只写出结论).
已知椭圆 的一个顶点是
的一个顶点是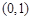 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆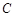 的方程;
的方程;
(Ⅱ)已知矩形 的四条边都与椭圆
的四条边都与椭圆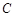 相切,设直线AB方程为
相切,设直线AB方程为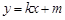 ,求矩形
,求矩形 面积的最小值与最大值.
面积的最小值与最大值.
如图, 已知边长为2的的菱形 与菱形
与菱形 全等,且
全等,且 ,平面
,平面 平面
平面 ,点
,点 为
为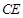 的中点.
的中点.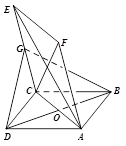
(Ⅰ)求证: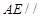 平面
平面 ;
;
(Ⅱ)求证: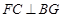 ;
;
(Ⅲ)求三棱锥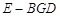 的体积.
的体积.
某校高三年级共有300人参加数学期中考试,从中随机抽取4名男生和4名女生的试卷,获得某一道题的样本,该题得分的茎叶图如图。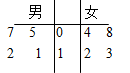
(Ⅰ)求样本的平均数;
(Ⅱ)设该题得分大于样本的平均数为合格,根据样本数据估计该校高三年级有多少名同学此题成绩合格;
(Ⅲ)在这4名男生和4名女生中,分别随机抽取一人,求该题女生得分不低于男生得分的概率.
已知数列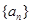 为等差数列,
为等差数列,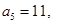 且
且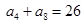 .
.
(Ⅰ)求数列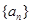 的通项;
的通项;
(Ⅱ)设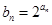
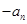 ,求数列
,求数列 的前
的前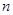 项和
项和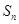 .
.